题目内容
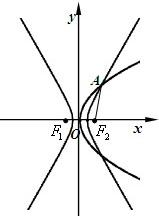
如图,双曲线C1: 与椭圆C2:
与椭圆C2: (0<b<2)的左、右顶点分别为A1、A2第一象限内的点P在双曲线C1上,线段OP与椭圆C2交于点A,O为坐标原点.
(0<b<2)的左、右顶点分别为A1、A2第一象限内的点P在双曲线C1上,线段OP与椭圆C2交于点A,O为坐标原点.(I)求证:
 为定值(其中
为定值(其中 表示直线AA1的斜率,
表示直线AA1的斜率, 等意义类似);
等意义类似);(II)证明:△OAA2与△OA2P不相似.
(III)设满足{(x,y)|
 ,x∈R,y∈R}⊆{(x,y)|
,x∈R,y∈R}⊆{(x,y)| ,x∈R,y∈R} 的正数m的最大值是b,求b的值.
,x∈R,y∈R} 的正数m的最大值是b,求b的值.
【答案】分析:(I)先求出A1A2的坐标,再设出A、P的坐标,利用两点连线的斜率公式结合两圆锥曲线的方程,将 进行化简,可证出
进行化简,可证出 为定值-1;
为定值-1;
(II)设 ,可得P(x,y),A(tx,ty),将此坐标分别代入椭圆和双曲线方程,联解可将OA•OP-OA22这个式子化简为关于t的函数f(t),利用函数f(t)为单调减函数的性质,可证出
,可得P(x,y),A(tx,ty),将此坐标分别代入椭圆和双曲线方程,联解可将OA•OP-OA22这个式子化简为关于t的函数f(t),利用函数f(t)为单调减函数的性质,可证出 故:△OAA2与△OA2P不相似.
故:△OAA2与△OA2P不相似.
(III)将双曲线方程与子集中的方程联解,化简得 ,因此对任意y不等于零,均有
,因此对任意y不等于零,均有 ,故
,故 ,可得m2≤3成立,因此因此b的值为
,可得m2≤3成立,因此因此b的值为 .
.
解答: (I)解:由已知得A1(-2,0),A2(2,0).
(I)解:由已知得A1(-2,0),A2(2,0).
设A(x1,y1),P(x2,y2),由题意知A、P均在第一象限,
且满足 ,
, .
.
则 =
= …(3分)
…(3分)
而Q、O、A、P在同一直线上,所以x1y2=x2y1
故 …(4分)
…(4分)
(II)证明:设 ,P(x,y),则A(tx,ty)且
,P(x,y),则A(tx,ty)且 ,
,
解之得: ,且
,且 …(6分)
…(6分)
OA•OP-OA22=tOP2-OA22= ,其中0<t<1
,其中0<t<1
所以f′(t)= 恒成立,,函数f(t)在区间(0,1)上是减函数,
恒成立,,函数f(t)在区间(0,1)上是减函数,
因此当0<t<1时,f(t)>f(1)= ,即
,即
故:△OAA2与△OA2P不相似.…(9分)
(III)解:由 得
得 ,由
,由 得
得 .
.
∴{(x,y)| ,x∈R,y∈R}⊆{(x,y)|
,x∈R,y∈R}⊆{(x,y)| ,x∈R,y∈R}
,x∈R,y∈R}
因此?y≠0, ?
? ?m2≤3所以b=
?m2≤3所以b=
因此b的值为 …(13分)
…(13分)
点评:本题考查了圆方程、直线方程、圆锥曲线的基本量和圆与圆锥曲线的关系等知识点,属于难题.解决本题一方面要求对圆方程、直线方程、圆锥曲线的方程有熟悉的理解,另一方面要求对含有字母的代数式化简、计算要精确到位,具有较强的综合性.
 进行化简,可证出
进行化简,可证出 为定值-1;
为定值-1;(II)设
 ,可得P(x,y),A(tx,ty),将此坐标分别代入椭圆和双曲线方程,联解可将OA•OP-OA22这个式子化简为关于t的函数f(t),利用函数f(t)为单调减函数的性质,可证出
,可得P(x,y),A(tx,ty),将此坐标分别代入椭圆和双曲线方程,联解可将OA•OP-OA22这个式子化简为关于t的函数f(t),利用函数f(t)为单调减函数的性质,可证出 故:△OAA2与△OA2P不相似.
故:△OAA2与△OA2P不相似.(III)将双曲线方程与子集中的方程联解,化简得
 ,因此对任意y不等于零,均有
,因此对任意y不等于零,均有 ,故
,故 ,可得m2≤3成立,因此因此b的值为
,可得m2≤3成立,因此因此b的值为 .
.解答:
 (I)解:由已知得A1(-2,0),A2(2,0).
(I)解:由已知得A1(-2,0),A2(2,0).设A(x1,y1),P(x2,y2),由题意知A、P均在第一象限,
且满足
 ,
, .
.则
 =
= …(3分)
…(3分)而Q、O、A、P在同一直线上,所以x1y2=x2y1
故
 …(4分)
…(4分)(II)证明:设
 ,P(x,y),则A(tx,ty)且
,P(x,y),则A(tx,ty)且 ,
,解之得:
 ,且
,且 …(6分)
…(6分)OA•OP-OA22=tOP2-OA22=
 ,其中0<t<1
,其中0<t<1所以f′(t)=
 恒成立,,函数f(t)在区间(0,1)上是减函数,
恒成立,,函数f(t)在区间(0,1)上是减函数,因此当0<t<1时,f(t)>f(1)=
 ,即
,即
故:△OAA2与△OA2P不相似.…(9分)
(III)解:由
 得
得 ,由
,由 得
得 .
.∴{(x,y)|
 ,x∈R,y∈R}⊆{(x,y)|
,x∈R,y∈R}⊆{(x,y)| ,x∈R,y∈R}
,x∈R,y∈R}因此?y≠0,
 ?
? ?m2≤3所以b=
?m2≤3所以b=
因此b的值为
 …(13分)
…(13分)点评:本题考查了圆方程、直线方程、圆锥曲线的基本量和圆与圆锥曲线的关系等知识点,属于难题.解决本题一方面要求对圆方程、直线方程、圆锥曲线的方程有熟悉的理解,另一方面要求对含有字母的代数式化简、计算要精确到位,具有较强的综合性.

练习册系列答案
相关题目
 如图,抛物线C1:y2=8x与双曲线
如图,抛物线C1:y2=8x与双曲线 如图,双曲线C1:
如图,双曲线C1: 有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.
有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5. ,试求所有满足条件的点P的坐标.
,试求所有满足条件的点P的坐标.