摘要:6.如图.在五面体中.点是矩形的对角线的交点.面是等边三角形.棱. (1)证明//平面, (2)设.证明平面. 解:(1)证明:取CD中点M.连结OM. 在矩形ABCD中.. 又.则. 连结EM.于是四边形EFOM为平行四边形., 又平面CDE.EM平面CDE.FO∥平面CDE (2)证明:连结FM.由(1)和已知条件. 在等边△CDE中.且. 因此平行四边形EFOM为菱形.从而EO⊥FM而FM∩CD=M.∴CD⊥平面EOM. 从而CD⊥EO.而.所以EO⊥平面CDF. 考查直线与平面位置关系.要求掌握直线与平面平行.垂直的判定定理和性质定理.会运用 “转化 的方法判定直线和平面平行与垂直.
网址:http://m.1010jiajiao.com/timu_id_4353106[举报]
 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱EF∥BC且EF=
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱EF∥BC且EF=| 3 |
| 3 |
(1)证明:面EOF⊥平面CDF;
(2)求B到面CDF的距离;
(3)求BF与面CDF所成的角. 查看习题详情和答案>>

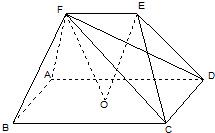 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱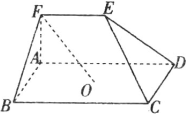 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,棱EF∥BC,
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,棱EF∥BC,