题目内容
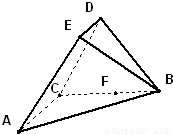
 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱EF∥BC且EF=
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱EF∥BC且EF=| 3 |
| 3 |
(1)证明:面EOF⊥平面CDF;
(2)求B到面CDF的距离;
(3)求BF与面CDF所成的角.
分析:法一:(1)设CD的中点为G,连接OG、EG,要证明面EOF⊥平面CDF,只需证明面EOF内的直线EO垂直平面CDF即可.
(2)EO⊥面CDF,所以B到面CDF的距离为O到面CDF的距离的两倍,求解即可.
(3)过F作面ABCD的垂线,垂足为H,由B到面CDF的距离,解三角形求BF与面CDF所成的角.
法二:建立空间直角坐标系,利用向量的数量积证明垂直,证明(1);
平面的法向量求出点到平面的距离,解答(2);
向量的数量积求出直线与平面所成的角,解答(3).
(2)EO⊥面CDF,所以B到面CDF的距离为O到面CDF的距离的两倍,求解即可.
(3)过F作面ABCD的垂线,垂足为H,由B到面CDF的距离,解三角形求BF与面CDF所成的角.
法二:建立空间直角坐标系,利用向量的数量积证明垂直,证明(1);
平面的法向量求出点到平面的距离,解答(2);
向量的数量积求出直线与平面所成的角,解答(3).
解答: 解:法一:(1)证明:设CD的中点为G,连接OG、EG
解:法一:(1)证明:设CD的中点为G,连接OG、EG
显然EF∥OG且EF=OG
∴四边形FOGE是平行四边形
∴FO∥EG,EF=OG=
BC=
CD
而△ECD是正三角形,
∴EG=
CD
∴平行四边形FOGE是菱形,EO⊥FG
又CD⊥OG,CD⊥EG,
∴CD⊥平面OGE,
而EO?平面OEG
,∴CD⊥EO
而FG与CD相交,故EO⊥平面CDF
∴面EOF⊥CDF
(2)EO⊥面CDF,
所以O到面CDF的距离为
OE=
又O为BD中点,
所以B到面CDF的距离为O到面CDF的距离的两倍
∴B到面CDF的距离为
(3)过F作面ABCD的垂线,垂足为H,
则HG=
,FH=
,BF2=BH2+FH2=1+(
)2+(
)2=4
由(2)B到面CDF的距离为
如果BF与面CDF所成的角θ,则sinθ=
=
∴BF与面CDF所成的角为
法二:(1)建立如图空间直角坐标系,
则C(1,
,0),D(-1,
,0),E(0,
,
),F(0,-
,
)
∵
∴OE⊥面CDF,
∴面EOF⊥面CDF
(2)∵B(1,-
,0),
=(-1,
,
) ∴d=
∴d=
=
=
(3)cos<
,
>=
=
∴BF与面CDF所成的角为
 解:法一:(1)证明:设CD的中点为G,连接OG、EG
解:法一:(1)证明:设CD的中点为G,连接OG、EG显然EF∥OG且EF=OG
∴四边形FOGE是平行四边形
∴FO∥EG,EF=OG=
| 1 |
| 2 |
| ||
| 2 |
而△ECD是正三角形,
∴EG=
| ||
| 2 |
∴平行四边形FOGE是菱形,EO⊥FG
又CD⊥OG,CD⊥EG,
∴CD⊥平面OGE,
而EO?平面OEG
,∴CD⊥EO
而FG与CD相交,故EO⊥平面CDF
∴面EOF⊥CDF
(2)EO⊥面CDF,
所以O到面CDF的距离为
| 1 |
| 2 |
| ||
| 2 |
又O为BD中点,
所以B到面CDF的距离为O到面CDF的距离的两倍
∴B到面CDF的距离为
| 3 |
(3)过F作面ABCD的垂线,垂足为H,
则HG=
3
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
由(2)B到面CDF的距离为
| 3 |
如果BF与面CDF所成的角θ,则sinθ=
| ||
| BF |
| ||
| 2 |
∴BF与面CDF所成的角为
| π |
| 3 |
法二:(1)建立如图空间直角坐标系,
则C(1,
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
∵
|
∴面EOF⊥面CDF
(2)∵B(1,-
| 3 |
| BF |
| ||
| 2 |
| 3 |
| 2 |
 ∴d=
∴d=
| ||||
|
|
| 3 | ||
|
| 3 |
(3)cos<
| BF |
| OE |
| ||||
|
|
| ||
| 2 |
∴BF与面CDF所成的角为
| π |
| 3 |
点评:本题考查直线与平面所成的角,平面与平面的垂直,点到平面的距离,既考查证明题又考查计算题,考查逻辑思维能力空间想象能力,是高考常考点,是中档题.

练习册系列答案
相关题目
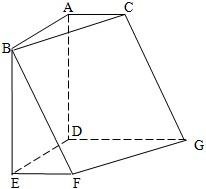 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1. 如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=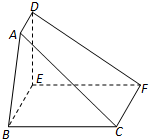 如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE.
如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE. ,AC=BC=2ED=2,AC⊥BC,且ED∥AC
,AC=BC=2ED=2,AC⊥BC,且ED∥AC  ,求二面角F-AE-B的余弦值.
,求二面角F-AE-B的余弦值.