网址：http://m.1010jiajiao.com/timu_id_4352321[举报]
已知关于x的一元二次方程－x2＋bx＋c＝0的两个实数根是m，4，其中0＜m＜4．
(1)求b，c的值(用含m的代数式表示)；
(2)设抛物线y＝－x2＋bx＋c与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C，如图所示，若点D的坐标为(0，－2)，且AD2＋BD2＝25，求抛物线的关系式及点C的坐标；
(3)在(2)中所得的抛物线上是否存在点P，使得PC＝PD？若存在，求出P点的坐标；若不存在，请说明理由；
(4)在(2)中所得的抛物线上是否存在点P，使得△PCD是等腰三角形？若存在，指出满足条件的P点的个数；若不存在，请说明理由．
已知：抛物线y＝x2－(2m＋4)x＋m2－10与x轴交于A、B两点，C是抛物线的顶点．
(1)用配方法求顶点C的坐标(用含m的代数式表示)；
(2)“若AB的长为2
，求抛物线的解析式．”解法的部分步骤如下，补全解题过程，并简述步骤①的解题依据，步骤②的解题方法．
解：由(1)知，对称轴与x轴交于点D( ，0)．
∵抛物线的对称性及AB＝2
，
∴AD＝BD＝|xA－xD|＝
．
∵点A(xA，0)在抛物线y＝(x－h)2＋k上，
∴0＝(xA－h)2＋k． ①
∵h＝xC＝xD，将|xA－xD|＝
代入上式，得到关于m的方程
0＝(
)2＋( ) ②
(3)将(2)中的条件“AB的长为2
”改为“△ABC为等边三角形”，用类似的方法求出此抛物线的解析式．
已知抛物线y＝x2－(2m＋4)x＋m2－10与x轴交于A、B两点，C是抛物线的顶点．
(1)用配方法求顶点C的坐标(用含有m的代数式表示)；
(2)“若AB的长为2
，求抛物线的解析式”的解法如下：
由(1)知，对称轴与x轴交于点D(________，0)．
∵抛物线具有对称性，且AB＝2
，
∴AD＝DB＝|xA－xD|＝．
∵A(xA，0)在抛物线y＝(x－h)2＋k上，
∴(xA－h)2＋k＝0． ①
∵h＝xC＝xD，
∴将|xA－xD|＝
代入①，得到关于m的方程0＝(
)2＋(________)． ②
补全解题过程，并简述步骤①的解题依据，步骤②的解题方法．
(3)将(2)中条件“AB的长为2
”改为“△ABC为等边三角形”，用类似的方法求出抛物线的解析式．
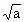(a＞0)，EM＝x．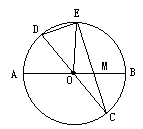
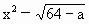·x＋12＝0；
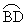上是否存在一点E，使EM的长是关于x的方程
－
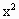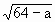·x＋12＝0的相等的实根，如果存在，求出sin∠EOM的值；如果不存在，请说明理由．