题目内容
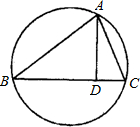
如图,在半径为4的圆O中,AB,CD是两条直径,M是OB的中点,CM的延长线交圆O于点E,设DE=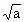 (a>0),EM=x.
(a>0),EM=x.
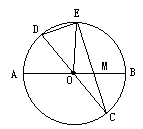
(1)用含x和a的代数式表示MC的长,并试证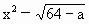 ·x+12=0;
·x+12=0;
(2)当a=15且EM>MC时,求sin∠EOM;
(3)根据图形写出EM长的取值范围;
(4)试问,在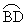 上是否存在一点E,使EM的长是关于x的方程
上是否存在一点E,使EM的长是关于x的方程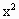 -
-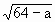 ·x+12=0的相等的实根,如果存在,求出sin∠EOM的值;如果不存在,请说明理由.
·x+12=0的相等的实根,如果存在,求出sin∠EOM的值;如果不存在,请说明理由.
答案:
解析:
解析:
|
解:(1)因为CD为圆O直径,所以∠DEC= 因为 又因为由相交弦定理EM·MC=AM·MB=12,所以MC= (2)当a=15时,方程为 因为EM>MC,所以EM=4,MC=3,由半径OE=4, 得△EOM为等腰三角形. 作EF⊥OM于F,则OF=FM=1,由勾股定理EF= (3)根据图形不难看出MB<EM<MA,所以2<EM<6. (4)假设 所以方程 因为2<EM=2 因为 所以△EOM为Rt△,∠OME= |

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|

 ,
, =
= ,MC=EC-EM=
,MC=EC-EM= -x.
-x. ,
, ,整理,得
,整理,得 +12=0.
+12=0. -7x+12=0,解得
-7x+12=0,解得 =4.
=4. =
= ,Rt△EOF中,sin∠EOM=
,Rt△EOF中,sin∠EOM= .
. 上存在一点E,使EM的长是方程
上存在一点E,使EM的长是方程 ·x+12=0的相等实根,由Δ=
·x+12=0的相等实根,由Δ= -4×12=0,得到64-a=48.
-4×12=0,得到64-a=48. .
. <6,所以在
<6,所以在 =4,所以
=4,所以 =
= .
. .
. 如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为
如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为 如图,在半径为6cm的圆中,弦AB长6
如图,在半径为6cm的圆中,弦AB长6 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是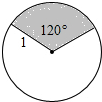 如图,在半径为1的圆中,圆心角为120°的扇形AOB的面积等于
如图,在半径为1的圆中,圆心角为120°的扇形AOB的面积等于