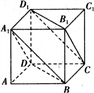
摘要:例1.正方体ABCD-A1B1C1D1中. (1)求证:平面A1BD∥平面B1D1C, (2)若E.F分别是AA1.CC1的中点.求证:平面EB1D1∥平面FBD. 证明:(1)由B1B∥DD1.得四边形BB1D1D是平行四边形. ∴B1D1∥BD. 又BD Ë平面B1D1C.B1D1平面B1D1C. ∴BD∥平面B1D1C. 同理A1D∥平面B1D1C. 而A1D∩BD=D. ∴平面A1BD∥平面B1CD. (2)由BD∥B1D1.得BD∥平面EB1D1. 取BB1中点G.∴AE∥B1G. 从而得B1E∥AG.同理GF∥AD. ∴AG∥DF. ∴B1E∥DF. ∴DF∥平面EB1D1. ∴平面EB1D1∥平面FBD. 说明 要证“面面平面 只要证“线面平面 .要证“线面平行 .只要证“线线平面 .故问题最终转化为证线与线的平行. 例2.在四面体中..且. 求证:平面⊥平面 例3.如图.为正三角形.平面..且.是的中点. 求证:(1),(2)平面平面,(3)平面平面. 例4三棱锥中..点为中点.于点.连.求证:平面平面
网址:http://m.1010jiajiao.com/timu_id_4057208[举报]
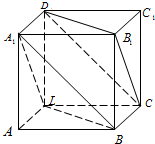 如图,在正方体ABCD-A1B1C1D1中,求证:平面A1BD∥平面CD1B1.
如图,在正方体ABCD-A1B1C1D1中,求证:平面A1BD∥平面CD1B1.