题目内容
如图,在正方体ABCD-A1B1C1D1 中,求证:平面A1BD ∥平面CB1D1 .
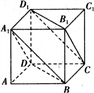
证明:以D 为原点,分别以DA 、DC 、DD1所在直线为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系,
设正方体的棱长为1,则A1(1,0,1),B(1,1,0),D(0,0,0),D1(0,0,1),B1(1,1,1),C(0,1,0).
 =(-1,0,-1),
=(-1,0,-1), =(0,1,-1),
=(0,1,-1), =(1,1,0),
=(1,1,0), =(0,1,-1).
=(0,1,-1).
设平面A1DB的法向量n1=(x,y,z),
则 得
得
令x=-1,则y=z=1,
∴平面A1DB的一个法向量n1=(-1,1,1).
同理,平面CB1D1的一个法向量n2=(1,-1,-1).
∴n1=-n2,即n1∥n2,
∴平面A1BD∥平面CB1D1.

设正方体的棱长为1,则A1(1,0,1),B(1,1,0),D(0,0,0),D1(0,0,1),B1(1,1,1),C(0,1,0).
 =(-1,0,-1),
=(-1,0,-1), =(0,1,-1),
=(0,1,-1), =(1,1,0),
=(1,1,0), =(0,1,-1).
=(0,1,-1).设平面A1DB的法向量n1=(x,y,z),
则
 得
得
令x=-1,则y=z=1,
∴平面A1DB的一个法向量n1=(-1,1,1).
同理,平面CB1D1的一个法向量n2=(1,-1,-1).
∴n1=-n2,即n1∥n2,
∴平面A1BD∥平面CB1D1.


练习册系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )