摘要：如图所示.在几何体ABCDE中.△ABC是等腰直角三角形.∠ABC=90°. BE和CD都垂直于平面ABC.且BE=AB=2.CD=1.点F是AE的中点. 求AB与平面BDF所成角的正弦值. 解 以点B为原点.BA.BC.BE所在的直线分别为x.y.z轴.建立如图所示的空间直角坐标系.则 B.C.E. ∴=.=. 设平面BDF的一个法向量为 n=. ∵n⊥.n⊥. ∴ 即 解得a=1.b=-2.∴n=. 设AB与平面BDF所成的角为.则法向量n与的夹角为-. ∴cos(-)===, 即sin=,故AB与平面BDF所成角的正弦值为.
网址：http://m.1010jiajiao.com/timu_id_4053326[举报]
如图所示，在几何体ABCDE中，△ABC是等腰直角三角形，∠ABC=90°，BE和CD都垂直于平面ABC，且BE=AB=2，CD=1，点F是AE的中点.求AB与平面BDF所成角的正弦值.
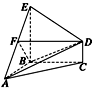
如图所示，在几何体ABCDE中，△ABC是等腰直角三角形，△ABC=90°，BE和CD都垂直于平面ABC，且BE=AB=2，CD=1，点F是AE的中点．
(1)证明：DF//平面ABC；
(2)求AB与平面BDF所成角的大小．
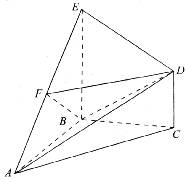
如图所示，在几何体ABCDE中，△ABC是等腰直角三角形，∠ABC=90°，BE和CD都垂直于平面ABC，且BE=AB=2，CD=1，点F是AE的中点.求AB与平面BDF所成角的正弦值.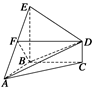
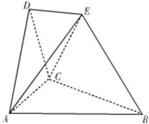在如图所示的空间几何体中，△ABC，△ACD都是等边三角形，AE=CE，DE∥平面ABC，平面ACD⊥平面ABC．
在如图所示的空间几何体中，△ABC，△ACD都是等边三角形，AE=CE，DE∥平面ABC，平面ACD⊥平面ABC．