题目内容
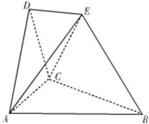在如图所示的空间几何体中，△ABC，△ACD都是等边三角形，AE=CE，DE∥平面ABC，平面ACD⊥平面ABC．（1）求证：DE⊥平面ACD；
（2）若AB=BE=2，求多面体ABCDE的体积．
分析：（1）要证DE⊥平面ACD，只需证明直线DE平垂直平面ACD内的两条相交直线AC、BO即可；
（2）若AB=BE=2，求多面体ABCDE的体积，转化为求三棱锥E-DAC的体积V1=
S△BAC•DE和V2=
S△AEC•EF之和即可．
（2）若AB=BE=2，求多面体ABCDE的体积，转化为求三棱锥E-DAC的体积V1=
| 1 |
| 3 |
| 1 |
| 3 |
解答：
解：（1）法一：△ABC，△ACD都是等边三角形，
AE=CE，取AC中点O，连接BO，DO，EO，则
BO⊥AC，DO⊥AC，EO⊥AC（2分）
∵EO∩BO=O，∴AC⊥平面OBF，
作EF⊥BO于点F，则AC⊥EF
∵AC∩BO=O，∴EF⊥平面ABC
∵平面ACD⊥平面ABC，
∴DO⊥平面ABC，BO⊥平面ACD，
∴DO∥EF
∴ODEF是平面四边形（4分）
∵DE∥平面ABC
∴OE∥OF，即DE∥OB
∴DE⊥平面ACD（6分）
法二：△ABC，△ACD都是等边三角形，
AE=CE，取AC中点O，连接BO，DO，EO，则
BO⊥AC，DO⊥AC，EO⊥AC（2分）∴AC⊥平面EDO，AC⊥平面OBE∴OB，OD，OE共面，即OB，OD，OE?平面OBED
又∵DE∥平面ABC，∴DE∥BO（4分）
∴DE⊥平面ACD（6分）
（2）由EF∥DO，DE∥OF，知DE=OF，EF=DO，
又AB=BE=2，△ABC，△ACD都是等边三角形，EF⊥BO
∴EF=DO=BO=
，BF=1，DE=CF=
-1（8分）
∵DE⊥平面ACD，∴三棱锥E-DAC的体积V1=
S△BAC•DE=
•
•(
-1)=
；
又三棱锥E-ABC的体积V2=
S△AEC•EF=
•
•
=1（11分）
∴多面体ABCDE的体积为V=V1+V2=
.（12分）
解：（1）法一：△ABC，△ACD都是等边三角形，AE=CE，取AC中点O，连接BO，DO，EO，则
BO⊥AC，DO⊥AC，EO⊥AC（2分）
∵EO∩BO=O，∴AC⊥平面OBF，
作EF⊥BO于点F，则AC⊥EF
∵AC∩BO=O，∴EF⊥平面ABC
∵平面ACD⊥平面ABC，
∴DO⊥平面ABC，BO⊥平面ACD，
∴DO∥EF
∴ODEF是平面四边形（4分）
∵DE∥平面ABC
∴OE∥OF，即DE∥OB
∴DE⊥平面ACD（6分）
法二：△ABC，△ACD都是等边三角形，
AE=CE，取AC中点O，连接BO，DO，EO，则
BO⊥AC，DO⊥AC，EO⊥AC（2分）∴AC⊥平面EDO，AC⊥平面OBE∴OB，OD，OE共面，即OB，OD，OE?平面OBED
又∵DE∥平面ABC，∴DE∥BO（4分）
∴DE⊥平面ACD（6分）
（2）由EF∥DO，DE∥OF，知DE=OF，EF=DO，
又AB=BE=2，△ABC，△ACD都是等边三角形，EF⊥BO
∴EF=DO=BO=
| 3 |
| 3 |
∵DE⊥平面ACD，∴三棱锥E-DAC的体积V1=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
3-
| ||
| 3 |
又三棱锥E-ABC的体积V2=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
∴多面体ABCDE的体积为V=V1+V2=
6-
| ||
| 3 |
点评：本题考查直线与平面垂直，棱锥的体积，考查空间想象能力，逻辑思维能力，是中档题．
练习册系列答案
相关题目
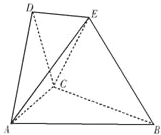在如图所示的空间几何体中，平面ACD⊥平面ABC，AB=BC=CA=DA=DC=BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在∠ABC的平分线上．
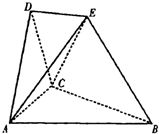在如图所示的空间几何体中，平面ACD⊥平面ABC，AB=BC=CA=DA=DC=BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在∠ABC的平分线上．
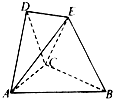在如图所示的空间几何体中，平面ACD⊥平面ABC．BE和平面ABC所成的角为
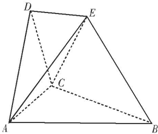在如图所示的空间几何体中，平面ACD⊥平面ABC，AB=BC=CA=DA=DC=BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在∠ABC的平分线上．