摘要: 设等差数列前项和满足.且.S2=6,函数.且 (1)求A, (2)求数列的通项公式, (3)若 中山市华侨中学2009年教师命题比赛数学科试题
网址:http://m.1010jiajiao.com/timu_id_4051971[举报]
设等差数列{an},{bn}前n项和Sn,Tn满足
=
,且
+
=
,S2=6;函数g(x)=
(x-1),且cn=g(cn-1)(n∈N,n>1),c1=1.
(1)求A;
(2)求数列{an}及{cn}的通项公式;
(3)若dn=
,试求d1+d2+…+dn.
查看习题详情和答案>>
| Sn |
| Tn |
| An+1 |
| 2n+7 |
| a3 |
| b4+b6 |
| a7 |
| b2+b8 |
| 2 |
| 5 |
| 1 |
| 2 |
(1)求A;
(2)求数列{an}及{cn}的通项公式;
(3)若dn=
|
设等差数列{an},{bn}前n项和Sn,Tn满足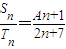 ,且
,且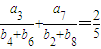 ,S2=6;函数
,S2=6;函数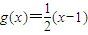 ,且cn=g(cn-1)(n∈N,n>1),c1=1.
,且cn=g(cn-1)(n∈N,n>1),c1=1.
(1)求A;
(2)求数列{an}及{cn}的通项公式;
(3)若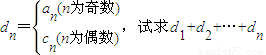 .
.
查看习题详情和答案>>
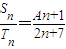 ,且
,且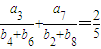 ,S2=6;函数
,S2=6;函数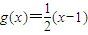 ,且cn=g(cn-1)(n∈N,n>1),c1=1.
,且cn=g(cn-1)(n∈N,n>1),c1=1.(1)求A;
(2)求数列{an}及{cn}的通项公式;
(3)若
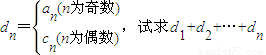 .
.查看习题详情和答案>>
在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,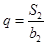 .(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足
.(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足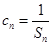 ,求{cn}的前n项和Tn.
,求{cn}的前n项和Tn.
【解析】本试题主要是考查了等比数列的通项公式和求和的运用。第一问中,利用等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,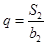 ,可得
,可得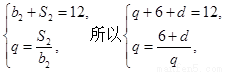 ,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,
,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,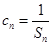 ,由第一问中知道
,由第一问中知道 ,然后利用裂项求和得到Tn.
,然后利用裂项求和得到Tn.
解: (Ⅰ) 设:{an}的公差为d,
因为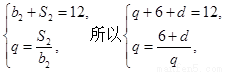 解得q=3或q=-4(舍),d=3.
解得q=3或q=-4(舍),d=3.
故an=3+3(n-1)=3n, bn=3 n-1. ………6分
(Ⅱ)因为 ……………8分
……………8分
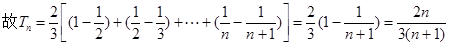
查看习题详情和答案>>
