题目内容
设等差数列{an},{bn}前n项和Sn,Tn满足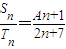 ,且
,且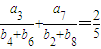 ,S2=6;函数
,S2=6;函数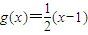 ,且cn=g(cn-1)(n∈N,n>1),c1=1.
,且cn=g(cn-1)(n∈N,n>1),c1=1.(1)求A;
(2)求数列{an}及{cn}的通项公式;
(3)若
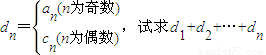 .
.
【答案】分析:(1)利用等差中项的概念,把 转化为
转化为 ,结合
,结合 得到
得到 ,从而A的值可求;
,从而A的值可求;
(2)由A=1,可令Sn=kn(n+1),由S2=6求出k,则Sn可求,分n=1和n≥2求得an.把给出的cn=g(cn-1)变形,得到数列{cn+1}是 为公比,以c1+1=2为首项的等比数列,由等比数列的通项公式求出cn+1,从而得到cn;
为公比,以c1+1=2为首项的等比数列,由等比数列的通项公式求出cn+1,从而得到cn;
(3)分n=2k和n=2k+1两类写出d1+d2+…+dn,然后利用分组求和.
解答:解:(1)∵{an},{bn}是等差数列,
由 ,得
,得 ,
,
而 ,
,
∴ ,解得A=1;
,解得A=1;
(2)令Sn=kn(n+1),∵S2=6,得6k=6,k=1,即 .
.
当n=1时,a1=S1=2,当n≥2时,an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n,
该式对n=1时成立,所以an=2n;
由题意 ,变形得
,变形得 (n≥2),
(n≥2),
∴数列{cn+1}是 为公比,以c1+1=2为首项的等比数列.
为公比,以c1+1=2为首项的等比数列.
 ,即
,即 ;
;
(3)当n=2k+1时,d1+d2+…+dn=(a1+a3+…a2k+1)+(c2+c4+…+c2k)
=[2+6+10+…+2(2k+1)]+[(1-1)+( )+…+(
)+…+( )]
)]
=
= .
.
当n=2k时,d1+d2+…+dn=(a1+a3+…a2k-1)+(c2+c4+…+c2k)
=[2+6+10+…+2(2k-1)]+[(1-1)+( )+…+(
)+…+( )]
)]
= .
.
综上: .
.
点评:本题考查了等差关系的确定,考查了等差数列的通项公式和等差中项概念,训练了分类讨论的数学思想方法,考查了数列的分组求和及等差数列和等比数列的前n项和公式,是中档题.
 转化为
转化为 ,结合
,结合 得到
得到 ,从而A的值可求;
,从而A的值可求;(2)由A=1,可令Sn=kn(n+1),由S2=6求出k,则Sn可求,分n=1和n≥2求得an.把给出的cn=g(cn-1)变形,得到数列{cn+1}是
 为公比,以c1+1=2为首项的等比数列,由等比数列的通项公式求出cn+1,从而得到cn;
为公比,以c1+1=2为首项的等比数列,由等比数列的通项公式求出cn+1,从而得到cn;(3)分n=2k和n=2k+1两类写出d1+d2+…+dn,然后利用分组求和.
解答:解:(1)∵{an},{bn}是等差数列,
由
 ,得
,得 ,
,而
 ,
,∴
 ,解得A=1;
,解得A=1;(2)令Sn=kn(n+1),∵S2=6,得6k=6,k=1,即
 .
.当n=1时,a1=S1=2,当n≥2时,an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n,
该式对n=1时成立,所以an=2n;
由题意
 ,变形得
,变形得 (n≥2),
(n≥2),∴数列{cn+1}是
 为公比,以c1+1=2为首项的等比数列.
为公比,以c1+1=2为首项的等比数列. ,即
,即 ;
;(3)当n=2k+1时,d1+d2+…+dn=(a1+a3+…a2k+1)+(c2+c4+…+c2k)
=[2+6+10+…+2(2k+1)]+[(1-1)+(
 )+…+(
)+…+( )]
)]=

=
 .
.当n=2k时,d1+d2+…+dn=(a1+a3+…a2k-1)+(c2+c4+…+c2k)
=[2+6+10+…+2(2k-1)]+[(1-1)+(
 )+…+(
)+…+( )]
)]=
 .
.综上:
 .
.点评:本题考查了等差关系的确定,考查了等差数列的通项公式和等差中项概念,训练了分类讨论的数学思想方法,考查了数列的分组求和及等差数列和等比数列的前n项和公式,是中档题.

练习册系列答案
相关题目