摘要:21.已知椭圆:(a>b>0)的中心在原点.焦点在轴上.离心率为.点F1.F2分别是椭圆的左.右焦点.在直线x=2上的点P(2, )满足|PF2|=|F1F2|.直线l:y=kx+m与椭圆C交于不同的两点A. B. (Ⅰ)求椭圆C的方程, (Ⅱ)若在椭圆C上存在点Q.满足(O为坐标原点).求实数l 的取值范围.
网址:http://m.1010jiajiao.com/timu_id_4047235[举报]
已知椭圆C:  (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆 上.
上.
(I)求椭圆C的方程;
(II)若斜率为k的直线过点M(2,0),且与椭圆C相交于A, B两点.试探讨k为何值时,三角形OAB为直角三角形.
查看习题详情和答案>>
已知椭圆 (a>b>0)的离心率e=
(a>b>0)的离心率e= ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l与椭圆相交于不同的两点A、B,已知点A的坐标为
(i)若 ,求直线l的倾斜角;
,求直线l的倾斜角;
(ii)若点Q 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且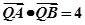 .求
.求 的值.
的值.
查看习题详情和答案>>
已知椭圆 (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。
(I)求椭圆的离心率。
(II)设A为椭圆的右顶点,O为坐标原点,若Q在椭圆上且满足|AQ|=|AO|,求直线OQ的斜率的值。
【考点定位】本小题主要考查椭圆的标准方程和几何性质、直线的方程、平面内两点间距离公式等基础知识. 考查用代数方法研究圆锥曲线的性质,以及数形结合的数学思想方法.考查运算求解能力、综合分析和解决问题的能力.
查看习题详情和答案>>