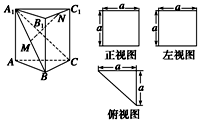
摘要:一个多面体的直观图和三视图如图所示.M.N分别为A1B.B1C1的中点.求证: (1)MN∥平面ACC1A1, (2)MN⊥平面A1BC. 证明 由题意可知.这个几何体是直三棱柱. 且AC⊥BC.AC=BC=CC1. (1)连接AC1.AB1. 由直三棱柱的性质得AA1⊥平面A1B1C1. 所以AA1⊥A1B1.则四边形ABB1A1为矩形. 由矩形性质得AB1过A1B的中点M. 在△AB1C1中.由中位线性质得MN∥AC1. 又AC1平面ACC1A1. MN平面ACC1A1. 所以MN∥平面ACC1A1. (2)因为BC⊥平面ACC1A1.AC1平面ACC1A1. 所以BC⊥AC1. 在正方形ACC1A1中.A1C⊥AC1. 又因为BC∩A1C=C. 所以AC1⊥平面A1BC. 由MN∥AC1.得MN⊥平面A1BC.
网址:http://m.1010jiajiao.com/timu_id_4039544[举报]
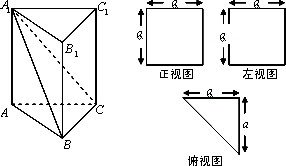
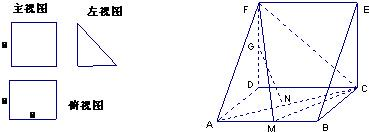 一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.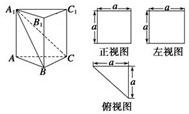 一个多面体的直观图和三视图(正视图、左视图、俯视图)如图所示,则三棱锥
一个多面体的直观图和三视图(正视图、左视图、俯视图)如图所示,则三棱锥