摘要：22． 已知定点A(a.O)( a >0).直线l1 : y=-a交y轴于点B.记过点A且与直线l1相切的圆的圆心为点C． (I)求动点C的轨迹E的方程, (Ⅱ)设倾斜角为α的直线l2过点A.交轨迹E于两点 P.Q.交直线l1于点R． (1)若tanα=1.且ΔPQB的面积为.求a的值, (2)若α∈[.].求|PR|·|QR|的最小值． 2009年福建省普通高中毕业班质量检查
网址：http://m.1010jiajiao.com/timu_id_4037576[举报]
（本小题满分14分）已知直线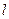
:y=k(x+2
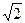)与圆O：x2+y2=4相交于不重合的
A、B两点，O是坐标原点，且三点A、B、O构成三角形．
（1）求k的取值范围；
（2）三角形ABO的面积为S，试将S表示成k的函数，并求出它的定义域；
（3）求S的最大值，并求取得最大值时k的值．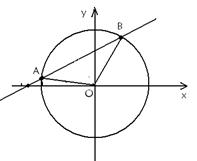
（本小题满分14分）
已知函数
（Ⅰ）求f(x)在［-1，e］（e为自然对数的底数）上的最大值；
（Ⅱ）对任意给定的正实数a，曲线y= f(x)上是否存在两点P，Q，使得△POQ是以O为直角顶点的直角三角形，且此三角形斜边中点在y轴上？
查看习题详情和答案>>
（本小题满分14分）已知动圆与直线
相切，且过定点F(1, 0)，动圆圆心为M．
（1）求点M的轨迹C的方程；
（2）若直线l与曲线C交于A、B两点，且
（O为坐标原点），求证：直线l过一定点．
查看习题详情和答案>>
:y=k(x+2
)与圆O：x2+y2=4相交于不重合的
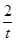)(t∈R , t≠ 0)为圆心的圆与
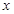轴交于点O, A，
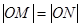，求圆C的方程．