摘要:已知向量a=,|b|=1,且a与b满足|ka+b|=|a-kb| . (1)试用k表示a·b.并求a·b的最小值, (2)若0≤x≤,b=,求a·b的最大值及相应的x值. 解(1)∵|a|=1.|b|=1. 由|ka+b|=|a-kb|, 得2=32, 整理得a·b==≥, 当且仅当k=1时.a·b取最小值. (2)由a·b=cosx+sinx=sin(x+). ∵0≤x≤.∴≤x+≤. ∴-≤sin(x+)≤1. 当x=时.a·b取最大值为1.
网址:http://m.1010jiajiao.com/timu_id_4033577[举报]
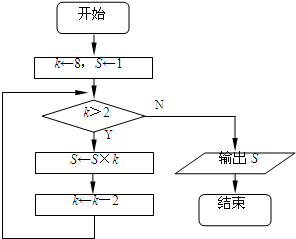 (2008•南京模拟)如图所示的流程图输出的结果是
(2008•南京模拟)如图所示的流程图输出的结果是