摘要:题型1:空间向量的概念及性质 例1.有以下命题:①如果向量与任何向量不能构成空间向量的一组基底.那么的关系是不共线,②为空间四点.且向量不构成空间的一个基底.那么点一定共面,③已知向量是空间的一个基底.则向量.也是空间的一个基底.其中正确的命题是 ①② ①③ ②③ ①②③ 解析:对于①“如果向量与任何向量不能构成空间向量的一组基底.那么的关系一定共线 ,所以①错误.②③正确. 点评:该题通过给出命题的形式考察了空间向量能成为一组基的条件.为此我们要掌握好空间不共面与不共线的区别与联系. 例2.下列命题正确的是 若与共线.与共线.则与共线, 向量共面就是它们所在的直线共面, 零向量没有确定的方向, 若.则存在唯一的实数使得, 解析:A中向量为零向量时要注意.B中向量的共线.共面与直线的共线.共面不一样.D中需保证不为零向量. 答案C. 点评:零向量是一个特殊的向量.时刻想着零向量这一特殊情况对解决问题有很大用处.像零向量与任何向量共线等性质.要兼顾. 题型2:空间向量的基本运算 例3.如图:在平行六面体中.为与的交点.若...则下列向量中与相等的向量是( ) 解析:显然, 答案为A. 点评:类比平面向量表达平面位置关系过程.掌握好空间向量的用途.用向量的方法处理立体几何问题.使复杂的线面空间关系代数化.本题考查的是基本的向量相等.与向量的加法.考查学生的空间想象能力. 例4.已知:且不共面.若∥,求的值. 解:∥,,且即 又不共面, 点评:空间向量在运算时.注意到如何实施空间向量共线定理. 题型3:空间向量的坐标 例5.(1)已知两个非零向量=(a1.a2.a3).=(b1.b2.b3).它们平行的充要条件是( ) A. :||=:|| B.a1·b1=a2·b2=a3·b3 C.a1b1+a2b2+a3b3=0 D.存在非零实数k.使=k (2)已知向量=.=.若||=6.⊥.则x+y的值是( ) A. -3或1 B.3或-1 C. -3 D.1 (3)下列各组向量共面的是( ) A. =.=.= B. =.=.= C. =.=.= D. =.=.= 解析:(1)D,点拨:由共线向量定线易知, (2)A 点拨:由题知或, (3)A 点拨:由共面向量基本定理可得. 点评:空间向量的坐标运算除了数量积外就是考察共线.垂直时参数的取值情况. 例6.已知空间三点A.C.设=.=.(1)求和的夹角,(2)若向量k+与k-2互相垂直.求k的值. 思维入门指导:本题考查向量夹角公式以及垂直条件的应用.套用公式即可得到所要求的结果. 解:∵A.C.=.=. ∴=.=. (1)cos==-. ∴和的夹角为-. (2)∵k+=k=. k-2=.且(k+)⊥(k-2). ∴=+k2-8=2k2+k-10=0. 则k=-或k=2. 点拨:第(2)问在解答时也可以按运算律做.(+)(k-2)=k22-k·-22=2k2+k-10=0.解得k=-.或k=2. 题型4:数量积 例7.(2000江西.山西.天津理.4)设..c是任意的非零平面向量,且相互不共线,则 ①(·)-(·)= ②||-||<|-| ③(·)-(·)不与垂直 ④(3+2)(3-2)=9||2-4||2中.是真命题的有( ) A.①② B.②③ C.③④ D.②④ 答案:D 解析:①平面向量的数量积不满足结合律.故①假, ②由向量的减法运算可知||.||.|-|恰为一个三角形的三条边长.由“两边之差小于第三边 .故②真, ③因为[(·)-(·)]·=(·)·-(·)·=0.所以垂直.故③假, ④(3+2)(3-2)=9··-4·=9||2-4||2成立.故④真. 点评:本题考查平面向量的数量积及运算律. 例8.已知向量和的夹角为120°.且||=2.||=5.则(2-)·= . (2)设空间两个不同的单位向量=(x1.y1.0).=(x2.y2.0)与向量=的夹角都等于.(1)求x1+y1和x1y1的值,(2)求<.>的大小(其中0<<.><π. 解析:(1)答案:13,解析:∵(2-)·=22-·=2||2-||·||·cos120°=2·4-2·5(-)=13. ∵||=||=1.∴x+y=1.∴x=y=1. 又∵与的夹角为.∴·=||||cos==. 又∵·=x1+y1.∴x1+y1=. 另外x+y=(x1+y1)2-2x1y1=1.∴2x1y1=()2-1=.∴x1y1=. (2)cos<.>==x1x2+y1y2.由(1)知.x1+y1=.x1y1=.∴x1.y1是方程x2-x+=0的解. ∴或同理可得或 ∵≠.∴或 ∴cos<.>=·+·=+=. ∵0≤<.>≤π.∴<.>=. 评述:本题考查向量数量积的运算法则. 题型5:空间向量的应用 例9.(1)已知a.b.c为正数.且a+b+c=1.求证:++≤4. (2)已知F1=i+2j+3k.F2=-2i+3j-k.F3=3i-4j+5k.若F1.F2.F3共同作用于同一物体上.使物体从点M1移到点M2.求物体合力做的功. 解析:(1)设=(..).=. 则||=4.||=. ∵·≤||·||. ∴·=++≤||·||=4. 当==时.即a=b=c=时.取“= 号. (2)解:W=F·s=(F1+F2+F3)·=14. 点评:若=.=.则由·≤||·||.得2≤(a2+b2+c2)(x2+y2+z2).此式又称为柯西不等式(n=3).本题考查||·||≥·的应用.解题时要先根据题设条件构造向量..然后结合数量积性质进行运算.空间向量的数量积对应做功问题. 例10.如图,直三棱柱中,求证: 证明: 同理 又 设为中点,则 又 点评:从上述例子可以看出,利用空间向量来解决位置关系问题.要用到空间多边形法则.向量的运算.数量积以及平行,相等和垂直的条件.
网址:http://m.1010jiajiao.com/timu_id_4030666[举报]
设{
,
,
}是空间向量的一个单位正交基底,
=2
-4
+5
,
=
+2
-3
,则向量
,
的坐标分别为
查看习题详情和答案>>
| i |
| j |
| k |
| a |
| i |
| j |
| k |
| b |
| i |
| j |
| k |
| a |
| b |
(2,-4,5)(1,2,-3)
(2,-4,5)(1,2,-3)
.下面几种推理是类比推理的是 ( )
A.两条直线平行,同旁内角互补,如果 和
和 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则 
B.由平面向量的运算性质,推测空间向量的运算性质
C.某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员,;
D.一切偶数都能被2整除, 是偶数,所以
是偶数,所以 能被2整除
能被2整除
查看习题详情和答案>>
 [必做题]利用空间向量的方法解决下列问题:在正方体ABCD-A1B1C1D1中,E,F分别是BB1,DC的中点.
[必做题]利用空间向量的方法解决下列问题:在正方体ABCD-A1B1C1D1中,E,F分别是BB1,DC的中点. ,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.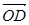 的坐标;
的坐标;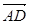 和
和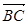 的夹角为θ,求cosθ的值
的夹角为θ,求cosθ的值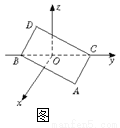
 和
和 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则
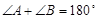
 是偶数,所以
是偶数,所以