题目内容
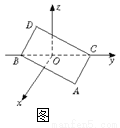
(12分)如图在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是( ,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
(1)求向量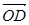 的坐标;
的坐标;
(2)设向量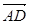 和
和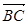 的夹角为θ,求cosθ的值
的夹角为θ,求cosθ的值
【答案】
(1{0,- };(2)
};(2) 。
。
【解析】
试题分析:(1)过D作DE⊥BC,垂足为E,在Rt△BDC中,由∠BDC=90°,∠DCB=30°,BC=2,得BD=1,CD= ,∴DE=CD·sin30°=
,∴DE=CD·sin30°= .
.
OE=OB-BE=OB-BD·cos60°=1- .
.
∴D点坐标为(0,- ),即向量
),即向量 的坐标为{0,-
的坐标为{0,- }.
}.
(2)依题意: ,
,
所以 .
.
设向量 和
和 的夹角为θ,则
的夹角为θ,则
cosθ=
 .
.
考点:本题主要考查向量的坐标运算、数量积及其夹角公式的应用。
点评:在空间直角坐标系中,将距离、夹角的计算问题转化成坐标运算。基本思路是“建系-坐标运算-模、夹角”。

练习册系列答案
相关题目
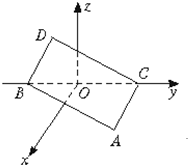 如图在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(
如图在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(
 ,
, ,则直线
,则直线 与直线
与直线 夹角的余弦值为(
)
夹角的余弦值为(
)
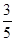 B.
B. C.
C. D.
D.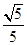
 ),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.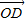 的坐标;
的坐标;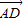 和
和 的夹角为θ,求cosθ的值.
的夹角为θ,求cosθ的值.