摘要：2． 距离 (1)两点间距离:若.则 特别地:轴.则.轴.则. (2)平行线间距离:若. 则:.注意点:x.y对应项系数应相等. (3)点到直线的距离:.则P到l的距离为:
网址：http://m.1010jiajiao.com/timu_id_4030362[举报]
定义变换T：
可把平面直角坐标系上的点P（x，y）变换到这一平面上的点P′（x′，y′）．特别地，若曲线M上一点P经变换公式T变换后得到的点P'与点P重合，则称点P是曲线M在变换T下的不动点．
（1）若椭圆C的中心为坐标原点，焦点在x轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2．求该椭圆C的标准方程．并求出当
时，其两个焦点F1、F2经变换公式T变换后得到的点F1′和F2′的坐标；
（2）当
时，求（1）中的椭圆C在变换T下的所有不动点的坐标；
（3）试探究：中心为坐标原点、对称轴为坐标轴的双曲线在变换T：
（
，k∈Z）下的不动点的存在情况和个数．
查看习题详情和答案>>
可把平面直角坐标系上的点P（x，y）变换到这一平面上的点P′（x′，y′）．特别地，若曲线M上一点P经变换公式T变换后得到的点P'与点P重合，则称点P是曲线M在变换T下的不动点．（1）若椭圆C的中心为坐标原点，焦点在x轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2．求该椭圆C的标准方程．并求出当时，其两个焦点F1、F2经变换公式T变换后得到的点F1′和F2′的坐标；（2）当
时，求（1）中的椭圆C在变换T下的所有不动点的坐标；（3）试探究：中心为坐标原点、对称轴为坐标轴的双曲线在变换T：
（，k∈Z）下的不动点的存在情况和个数．查看习题详情和答案>>
定义变换T：
可把平面直角坐标系上的点P（x，y）变换到这一平面上的点P′（x′，y′）．特别地，若曲线M上一点P经变换公式T变换后得到的点P'与点P重合，则称点P是曲线M在变换T下的不动点．
（1）若椭圆C的中心为坐标原点，焦点在x轴上，且焦距为2
，长轴顶点和短轴顶点间的距离为2．求该椭圆C的标准方程．并求出当θ=arctan
时，其两个焦点F1、F2经变换公式T变换后得到的点F1′和F2′的坐标；
（2）当θ=arctan
时，求（1）中的椭圆C在变换T下的所有不动点的坐标；
（3）试探究：中心为坐标原点、对称轴为坐标轴的双曲线在变换T：
（θ≠
，k∈Z）下的不动点的存在情况和个数．
查看习题详情和答案>>
|
（1）若椭圆C的中心为坐标原点，焦点在x轴上，且焦距为2
| 2 |
| 3 |
| 4 |
（2）当θ=arctan
| 3 |
| 4 |
（3）试探究：中心为坐标原点、对称轴为坐标轴的双曲线在变换T：
|
| kπ |
| 2 |
（本题满分18分，其中第1小题6分，第2小题4分，第3小题8分）
定义变换
：
可把平面直角坐标系上的点
变换到这一平面上的点
.特别地，若曲线
上一点
经变换公式变换后得到的点
与点重合，则称点是曲线在变换下的不动点.
（1）若椭圆
的中心为坐标原点，焦点在
轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2. 求该椭圆的标准方程. 并求出当
时，其两个焦点
、
经变换公式变换后得到的点
和
的坐标；
（2）当时，求（1）中的椭圆在变换下的所有不动点的坐标；
（3）试探究：中心为坐标原点、对称轴为坐标轴的双曲线在变换
：（
，
）下的不动点的存在情况和个数.
：
可把平面直角坐标系上的点
变换到这一平面上的点
.特别地，若曲线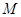
上一点
经变换公式
与点
的中心为坐标原点，焦点在
轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2. 求该椭圆
时，其两个焦点
、
经变换公式
和
的坐标；
，
）下的不动点的存在情况和个数.
：
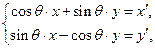可把平面直角坐标系上的点
变换到这一平面上的点
.特别地，若曲线
上一点
经变换公式
与点
的中心为坐标原点，焦点在
轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2. 求该椭圆
时，其两个焦点
、
经变换公式
和
的坐标；
，
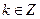）下的不动点的存在情况和个数.