摘要:例1 已知数列- (1)计算S1.S2.S3.S4. (2)猜想Sn的表达式.并证明. (3)Sn. 解:(1)S1=. S2= S3= S4=. (2 )解:通项是以3n-2.3n+1两数乘积为分母的.而我们看到.在表示上面四个结果的分数中.分子可用项数n表示.分母可用3n+1表示.于是可猜想. Sn= 证明方法一:用数学归纳法证明如下: 1° 当n=1时.S1=等式成立. 2° 假设当n=k时等式成立.即 Sk=. 当n=k+1时. ∴当n=k+1时.等式也成立. ∴Sn= (n∈N*) 证明方法二: ∴ ∴Sn= (3)解: 例2 已知下列极限.求a与b. (1) (2) (3) 分析:此题属于已知x趋向于x0时.函数的极限存在且等于某个常数.求函数关系式的类型.上边三个小题都不能简单地将x=x0直接代入函数的解析式中.因为中的x不趋于确定的常数.(3)虽然趋于1.但将x=1代入函数关系式中.分母为零.因此.解决此类问题的关键.是先要确定用哪种方法求极限.再将函数的解析式进行适当的变形.然后根据所给的条件进行分析.进而确定a.b的值. 解:(1) 1° 如果1-a≠0. ∵ ∴不存在. 2° 如果 1-a=0. ∵
网址:http://m.1010jiajiao.com/timu_id_4029628[举报]
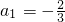 ,满足
,满足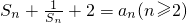 ,计算S1,S2,S3,S4,并猜想Sn的表达式.
,计算S1,S2,S3,S4,并猜想Sn的表达式.