摘要:如图所示.在长方体ABCD-A1B1C1D1中.AB=BC=1.BB1=2. E是棱CC1上的点.且CE=CC1. (1)求三棱锥C-BED的体积, (2)求证:A1C⊥平面BDE. (1)解 ∵CE=CC1=. ∴VC-BDE=VE-BCD=S△BCD·CE =××1×1×=. (2)证明 连接AC.B1C. ∵AB=BC.∴BD⊥AC. ∵A1A⊥底面ABCD, ∴BD⊥A1A. ∵A1A∩AC=A. ∴BD⊥平面A1AC. ∴BD⊥A1C. ∵tan∠BB1C==, tan∠CBE==,∴∠BB1C=∠CBE. ∵∠BB1C+∠BCB1=90°, ∴∠CBE+∠BCB1=90°,∴BE⊥B1C. ∵BE⊥A1B1.A1B1∩B1C=B1. ∴BE⊥平面A1B1C.∴BE⊥A1C. ∵BD∩BE=B.BE平面BDE.BD平面BDE. ∴A1C⊥平面BDE.
网址:http://m.1010jiajiao.com/timu_id_4024367[举报]
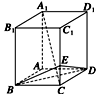


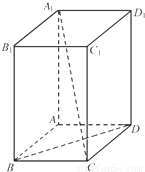
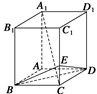
 CC1.
CC1.