Question

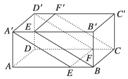
如图所示，在长方体ABCD-A₁B₁C₁D₁中，AB=BC=1，BB₁=2，连结A₁C、BD．
（Ⅰ）求证：A₁C⊥BD；
（Ⅱ）求三棱锥A₁-BCD的体积．

Answer 1

（Ⅰ）证明：连AC．
∵AB=BC，
∴BD⊥AC．                                             …（2分）
∵A₁A⊥底面ABCD，
∴BD⊥A₁A．                    …（4分）
∵A₁A?平面A₁AC，AC?平面A₁AC，A₁A∩AC=A，
∴BD⊥平面A₁AC．              …（6分）
∴BD⊥A₁C．                    …（8分）
（Ⅱ）∵A₁A⊥平面BCD，所以A₁A是锥体的高，
∴VA1-BCD=

1

3

S△BCD•AA1=

1

3

×

1

2

×1×1×2=

1

3

．…（14分）