摘要：已知f(x)是定义在［-1.1］上的奇函数.且f(1)=1,若a,b∈［-1,1］,a+b≠0时.有＞0. (1)判断函数f(x)在［-1.1］上是增函数.还是减函数.并证明你的结论, (2)解不等式:f(x+)＜f(); (3)若f(x)≤m2-2pm+1对所有x∈［-1,1］,p∈［-1,1］(p是常数)恒成立.求实数m的取值范围. 预习训练答案:
网址：http://m.1010jiajiao.com/timu_id_4023631[举报]
已知函数f(x)在(－∞,0)∪(0,+∞)上有定义，且在(0,+∞)上是增函数，f(1)=0,又g(θ)=sin2θ－mcosθ－2m,θ∈［0,
］,设M={m|g(θ)<0,m∈R},N={m|f［g(θ)］<0},求M∩N.
已知函数y=f(x)是定义在R上的函数，对于任意
，函数y=f(x)(－1≤x≤1)是奇函数，又知y=f(x)在［0，1］上是一次函数，在［1，4］上是二次函数，且在x=2时，函数取得最小值，最小值为－5.
(1)证明：f(1)+f(4)=0;
(2)试求y=f(x),x∈［1,4］的解析式；
查看习题详情和答案>> 已知函数f(x)在(－∞,0)∪(0,+∞)上有定义，且在(0,+∞)上是增函数，f(1)=0,又g(θ)=sin2θ－mcosθ－2m,θ∈［0,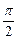
］,设M={m|g(θ)<0,m∈R},N={m|f［g(θ)］<0},求M∩N.
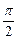］,设M={m|g(θ)<0,m∈R},N={m|f［g(θ)］<0},求M∩N.
| |||||||||
［0,1］时，f（x）＝
－x，若g（x）＝f（x）－m（x＋1）在区间（－1,2］有3个零点，则实数m的取值范围是（ ）.
，
）
B.（－
D.