摘要:熟记基本导数公式,
网址:http://m.1010jiajiao.com/timu_id_4023428[举报]
已知函数f(x)=ax2+ln(x+1).
(1)求函数g(x)=f(x)-ax2-x的单调区间及最大值;
(2)当x∈[0,+∞)时,不等式f(x)≤x恒成立,求实数a的取值范围.
(3)求证:(1+
)(1+
)(1+
)(1+
)…(1+
)<e
参考导数公式:(ln(x+1))′=
.
查看习题详情和答案>>
(1)求函数g(x)=f(x)-ax2-x的单调区间及最大值;
(2)当x∈[0,+∞)时,不等式f(x)≤x恒成立,求实数a的取值范围.
(3)求证:(1+
| 1 |
| 22 |
| 1 |
| 3^ |
| 1 |
| 42 |
| 1 |
| 52 |
| 1 |
| n2 |
参考导数公式:(ln(x+1))′=
| 1 |
| x+1 |
已知函数f(x)=-x3+3x2+9x+a.
(1)求f(x)的单调递减区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
思路 本题考查多项式的导数公式及运用导数求函数的单调区间和函数的最值,题目中需注意应先比较f(2)和f(-2)的大小,然后判定哪个是最大值从而求出a.
查看习题详情和答案>>
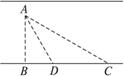
如图,一艘渔船停泊在距岸9 km 的A处,今需派人送信给距渔船3 km处的海岸渔站C,若送信人步行速度为每小时5 km,船速为每小时4 km,问在何处上岸,可以使抵站的时间最省?[参考导数公式(
km处的海岸渔站C,若送信人步行速度为每小时5 km,船速为每小时4 km,问在何处上岸,可以使抵站的时间最省?[参考导数公式( )′=
)′= ·
· ]
]
 ;
; ; (2)求
; (2)求 的最大值与最小值.
的最大值与最小值.