摘要:21.已知函数(1)若在上单调递增.求的取值范围,(2)若定义在区间D上的函数对于区间上的任意两个值总有以下不等式成立.则称函数为区间上的 “凹函数 .试证:当时.为“凹函数 . 解(1)由.得 --------2分 函数为上单调函数. 若函数为上单调增函数.则在上恒成立.即不等式在上恒成立. 也即在上恒成立. ----4分令.上述问题等价于.而为在上的减函数.则.于是为所求. ----6分 (2)证明:由 得 ---------7分 --------8分 而 ① ------10分 又. ∴ ② ---11分 ∵ ∴. ∵ ∴ ③ -----------13分 由①.②.③得 即.从而由凹函数的定义可知函数为凹函数. ----14分
网址:http://m.1010jiajiao.com/timu_id_4021290[举报]
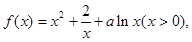
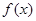 在
在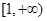 上单调递增,求
上单调递增,求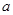 的取值范围;
的取值范围;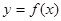 对于区间D上的任意两个值
对于区间D上的任意两个值 总有以下不等式
总有以下不等式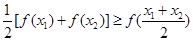 成立,则称函数
成立,则称函数 时,
时,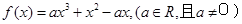
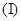 若函数
若函数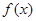 在
在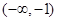 和
和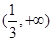 上是增函数,在
上是增函数,在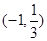 是减函数,求
是减函数,求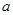 的值;
的值;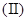 讨论函数
讨论函数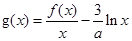 的单调递减区间;
的单调递减区间;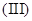 如果存在
如果存在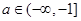 ,使函数
,使函数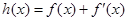 ,
,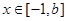
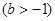 ,在
,在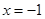 处取得最小值,试求
处取得最小值,试求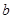 的最大值.
的最大值.
 若函数
若函数 在
在 和
和 上是增函数,在
上是增函数,在 是减函数,求
是减函数,求 的值;
的值; 讨论函数
讨论函数 的单调递减区间;
的单调递减区间; 如果存在
如果存在 ,使函数
,使函数 ,
,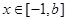
 ,在
,在 处取得最小值,试求
处取得最小值,试求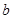 的最大值.
的最大值.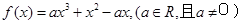
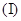 若函数
若函数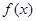 在
在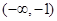 和
和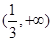 上是增函数,在
上是增函数,在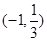 是减函数,求
是减函数,求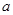 的值;
的值;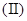 讨论函数
讨论函数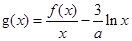 的单调递减区间;
的单调递减区间;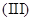 如果存在
如果存在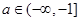 ,使函数
,使函数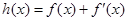 ,
,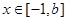
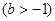 ,在
,在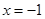 处取得最小值,试求
处取得最小值,试求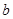 的最大值.
的最大值.