摘要:19. 已知函数的导函数的图象关于直线x=2对称. (Ⅰ)求b的值, (Ⅱ)若在处取得最小值.记此极小值为.求的定义域和值域. 解: (Ⅰ).因为函数的图象关于直线x=2对称. 所以.于是 知... (ⅰ)当c 12时..此时无极值. (ii)当c<12时.有两个互异实根,.不妨设<.则<2<. 当x<时.. 在区间内为增函数, 当<x<时..在区间内为减函数; 当时..在区间内为增函数. 所以在处取极大值.在处取极小值. 因此.当且仅当时.函数在处存在唯一极小值.所以. 于是的定义域为.由 得. 于是 . 当时.所以函数 在区间内是减函数.故的值域为
网址:http://m.1010jiajiao.com/timu_id_4017011[举报]
1. (本小题满分13分)
已知函数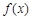 的导数
的导数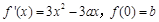 .a,b为实数,
.a,b为实数,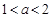 .
.
(1)
若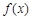 在区间
在区间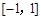 上的最小值、最大值分别为
上的最小值、最大值分别为 、1,求a、b的值;
、1,求a、b的值;
(2) 在 (1) 的条件下,求曲线在点P(2,1)处的切线方程;
(3)
设函数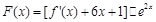 ,试判断函数
,试判断函数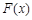 的极值点个数.
的极值点个数.
查看习题详情和答案>>
1. (本小题满分13分)
已知函数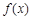 的导数
的导数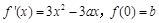 .a,b为实数,
.a,b为实数,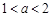 .
.
(1)
若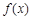 在区间
在区间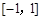 上的最小值、最大值分别为
上的最小值、最大值分别为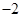 、1,求a、b的值;
、1,求a、b的值;
(2) 在 (1) 的条件下,求曲线在点P(2,1)处的切线方程.
查看习题详情和答案>>
(本小题满分13分)
已知函数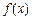 的导数
的导数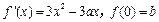 .a,b为实数,
.a,b为实数,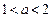 .
.
(1) 若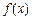 在区间
在区间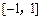 上的最小值、最大值分别为
上的最小值、最大值分别为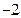 、1,求a、b的值;
、1,求a、b的值;
(2) 在 (1) 的条件下,求曲线在点P(2,1)处的切线方程;
(3) 设函数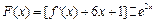 ,试判断函数
,试判断函数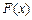 的极值点个数.
的极值点个数.
已知函数
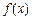 的导数
的导数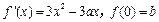 .a,b为实数,
.a,b为实数,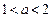 .
.(1) 若
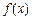 在区间
在区间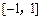 上的最小值、最大值分别为
上的最小值、最大值分别为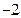 、1,求a、b的值;
、1,求a、b的值;(2) 在 (1) 的条件下,求曲线在点P(2,1)处的切线方程;
(3) 设函数
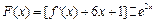 ,试判断函数
,试判断函数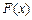 的极值点个数.
的极值点个数.