摘要：(1) 定义: (2)通项公式: (3)前n项和公式: (4)通项公式推广: 2.等差数列的一些性质 (1)对于任意正整数n.都有 (2)的通项公式 (3)对于任意的整数.如果.那么 (4)对于任意的正整数.如果.则 (5)对于任意的正整数n>1.有 (6)对于任意的非零实数b.数列是等差数列.则是等差数列 (7)已知是等差数列.则也是等差数列 (8)等都是等差数列 (9)是等差数列的前n项和.则 仍成等差数列.即 (10)若.则 (11)若.则 (12).反之也成立
网址：http://m.1010jiajiao.com/timu_id_4015530[举报]
定义：若数列{an}对任意n∈N*，满足
=k（k为常数），称数列{an}为等差比数列．
（1）若数列{an}前n项和Sn满足Sn=3（an-2），求{an}的通项公式，并判断该数列是否为等差比数列；
（2）若数列{an}为等差数列，试判断{an}是否一定为等差比数列，并说明理由；
（3）若数列{an}为等差比数列，定义中常数k=2，a2=3，a1=1，数列{
}的前n项和为Tn，求证：Tn＜3．
查看习题详情和答案>>
| an+2-an+1 |
| an+1-an |
（1）若数列{an}前n项和Sn满足Sn=3（an-2），求{an}的通项公式，并判断该数列是否为等差比数列；
（2）若数列{an}为等差数列，试判断{an}是否一定为等差比数列，并说明理由；
（3）若数列{an}为等差比数列，定义中常数k=2，a2=3，a1=1，数列{
| 2n-1 |
| an+1 |
定义：称
为n个正数p1，p2，…pn的“均倒数”．若已知数列{an}的前n项的“均倒数”为
．
（1）求数列{an}的通项公式；
（2）设cn=
，试判定数列{cn}的单调性；
（3）设dn=2n•an，试求数列{dn}的前n项和Tn．
查看习题详情和答案>>
| n |
| p1+p2+…+pn |
| 1 |
| 2n+1 |
（1）求数列{an}的通项公式；
（2）设cn=
| an |
| 2n+1 |
（3）设dn=2n•an，试求数列{dn}的前n项和Tn．
定义：称
为n个正数p1，p2，…pn的“均倒数”．若已知数列{an}的前n项的“均倒数”为
．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设dn=2n•an，试求数列{dn}的前n项和Tn．
查看习题详情和答案>>
| n |
| p1+p2+…+pn |
| 1 |
| 2n+1 |
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设dn=2n•an，试求数列{dn}的前n项和Tn．
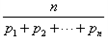为n个正数p1，p2，…，pn的“均倒数”。若已知数列{an}的前n项的“均倒数”为
，
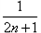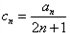，试判定数列{cn}的单调性；