摘要: 15.115°
网址:http://m.1010jiajiao.com/timu_id_4015019[举报]
甲、乙、丙三人射击同一目标,各射击一次,已知甲击中目标的概率为
,乙与丙击中目标的概率分别为m,n(m>n),每人是否击中目标是相互独立的.记目标被击中的次数为ξ,且ξ的分布列如下表:
(Ⅰ)求m,n的值;
(Ⅱ)求ξ的数学期望. 查看习题详情和答案>>
| 3 |
| 5 |
| ξ | 0 | 1 | 2 | 3 | ||||
| P |
|
a | b |
|
(Ⅱ)求ξ的数学期望. 查看习题详情和答案>>
甲、乙、丙三人射击同一目标,各射击一次,是否击中是相互独立的.将甲、乙、丙各自击中目标依次记为事件A,B,C,它们的对立事件分别记为
,
,
.若P(A)=
,P(ABC)=
,P(
)=
,且P(B)>P(C).
(Ⅰ) 求至少有一人击中目标的概率;
(Ⅱ) 求P(B)、P(C)的值. 查看习题详情和答案>>
. |
| A |
. |
| B |
. |
| C |
| 3 |
| 5 |
| 1 |
| 5 |
. |
| A |
. |
| B |
. |
| C |
| 1 |
| 15 |
(Ⅰ) 求至少有一人击中目标的概率;
(Ⅱ) 求P(B)、P(C)的值. 查看习题详情和答案>>
甲、乙、丙三人射击同一目标,各射击一次,已知甲击中目标的概率为
,乙与丙击中目标的概率分别为m,n(m>n),每人是否击中目标是相互独立的.记目标被击中的次数为ξ,且ξ的分布列如下表:
(Ⅰ)求m,n的值;
(Ⅱ)求ξ的数学期望.
查看习题详情和答案>>
| 3 |
| 5 |
| ξ | 0 | 1 | 2 | 3 | ||||
| P |
|
a | b |
|
(Ⅱ)求ξ的数学期望.
(2012•大丰市一模)数学家们在研究15、12、10这三个数的倒数时发现:
-
=
-
.因此就将具有这样性质的三个数称之为调和数,如6、3、2也是一组调和数.现有一组调和数:x、5、3(x>5),则x的值是
查看习题详情和答案>>
| 1 |
| 12 |
| 1 |
| 15 |
| 1 |
| 10 |
| 1 |
| 12 |
15
15
.2010年,我国部分地区手足口病流行,党和政府采取果断措施防、治结合,很快使病情得到控制.下表是某医院记载的5月1日到5月12日每天治愈者数据及根据数据绘制的散点图.
| 日期 | 5.1 | 5.2 | 5.3 | 5.4 | 5.5 | 5.6 |
| 人数 | 100 | 109 | 115 | 118 | 121 | 134 |
| 日期 | 5.7 | 5.8 | 5.9 | 5.10 | 5.11 | 5.12 |
| 人数 | 141 | 152 | 168 | 175 | 186 | 203 |
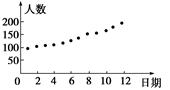
则下列说法:①根据此散点图,可以判断日期与治愈人数具有线性相关关系;②根据此散点图,可以判断日期与治愈人数具有一次函数关系;③根据此散点图,可以判断日期与治愈人数呈正相关.
其中正确的有
- A.0个
- B.1个
- C.2个
- D.3个