摘要:已知不等式对n∈N+都成立.则实数M的取值范围是 . 简答.提示:1-4.ADAB; 5. ax+ay≥2=2. ∵x-x2=-(x-)2≤.0<a<1.∴ax+ay≥2=2a. ∴loga(ax+ay)<loga2a=loga2+.即P<Q;
网址:http://m.1010jiajiao.com/timu_id_4009464[举报]
网址:http://m.1010jiajiao.com/timu_id_4009464[举报]
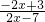 ,若存在实数x0,使f(x0)=x0则称x0是函数y=f(x)的一个不动点.
,若存在实数x0,使f(x0)=x0则称x0是函数y=f(x)的一个不动点. ≠
≠ 时,比较
时,比较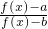 与
与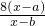 的大小;
的大小; 且an≠
且an≠ ,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式.
,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式.