题目内容
已知函数f(x)=x-1-lnx.
(1)求函数f(x)的最小值;
(2)求证:当n∈N*时,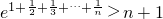 ;
;
(3)对于函数h(x)和g(x)定义域上的任意实数x,若存在常数k,b,使得不等式h(x)≥kx+b和g(x)≤kx+b都成立,则称直线y=kx+b是函数h(x)与g(x)的“分界线”.设函数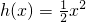 ,g(x)=e[x-1-f(x)],试问函数h(x)与g(x)是否存在“分界线”?若存在,求出常数k,b的值;若不存在,说明理由.
,g(x)=e[x-1-f(x)],试问函数h(x)与g(x)是否存在“分界线”?若存在,求出常数k,b的值;若不存在,说明理由.
(1)解:∵f(x)=x-1-lnx(x>0)
∴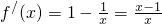 ,
,
当x∈(0,1)时,f′(x)<0,f(x)递减,
当x∈(1,+∞)时,f′(x)>0,f(x)递增,
∴f(x)的最小值为f(1)=0.…(4分)
(2)证明:由(1)知当x>0时恒有f(x)≥0,即x-1≥lnx,
∴ex-1≥x,从而有ex≥x+1,当且仅当x=0时取等号,…(6分)
分别令 ,
,
得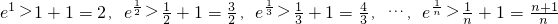 ,
,
相乘可得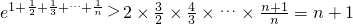 .…(8分)
.…(8分)
(3)解:令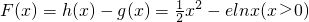 ,
,
则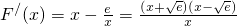 ,
,
当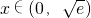 时,F′(x)<0,F(x)递减,
时,F′(x)<0,F(x)递减,
当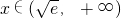 时,F′(x)>0,F(x)递增,
时,F′(x)>0,F(x)递增,
∴当 时F(x)取得最小值0,
时F(x)取得最小值0,
则h(x)与g(x)的图象在 处有公共点
处有公共点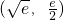 .…(10分)
.…(10分)
设函数h(x)与g(x)存在“分界线”,方程为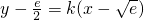 ,
,
应有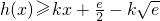 在x∈R时恒成立,
在x∈R时恒成立,
即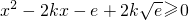 在x∈R时恒成立,
在x∈R时恒成立,
必须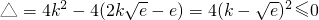 ,
,
得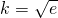 .…(13分)
.…(13分)
下证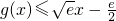 在x>0时恒成立,
在x>0时恒成立,
记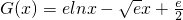 ,
,
则 ,当
,当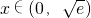 时,G′(x)>0,G(x)递增,
时,G′(x)>0,G(x)递增,
当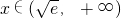 时,G′(x)<0,G(x)递减,
时,G′(x)<0,G(x)递减,
∴当 时G(x)取得最大值0,
时G(x)取得最大值0,
即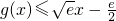 在x>0时恒成立,
在x>0时恒成立,
综上知,函数h(x)与g(x)存在“分界线”,其中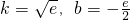 .…(16分)
.…(16分)
分析:(1)由f(x)=x-1-lnx(x>0)知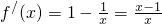 ,当x∈(0,1)时,f′(x)<0,f(x)递减,当x∈(1,+∞)时,f′(x)>0,f(x)递增,由此能求出f(x)的最小值.
,当x∈(0,1)时,f′(x)<0,f(x)递减,当x∈(1,+∞)时,f′(x)>0,f(x)递增,由此能求出f(x)的最小值.
(2)由(1)知当x>0时恒有f(x)≥0,即x-1≥lnx,故ex-1≥x,从而有ex≥x+1,当且仅当x=0时取等号,由此能够证明当n∈N*时,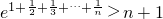 .
.
(3)令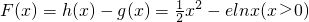 ,则
,则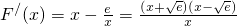 ,当
,当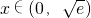 时,F′(x)<0,F(x)递减,当
时,F′(x)<0,F(x)递减,当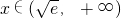 时,F′(x)>0,F(x)递增,故当
时,F′(x)>0,F(x)递增,故当 时F(x)取得最小值0,则h(x)与g(x)的图象在
时F(x)取得最小值0,则h(x)与g(x)的图象在 处有公共点
处有公共点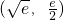 .由此能够导出函数h(x)与g(x)存在“分界线”,其中
.由此能够导出函数h(x)与g(x)存在“分界线”,其中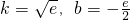 .
.
点评:本题考查利用导数求闭区间上函数最值的应用,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化.
∴
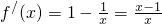 ,
,当x∈(0,1)时,f′(x)<0,f(x)递减,
当x∈(1,+∞)时,f′(x)>0,f(x)递增,
∴f(x)的最小值为f(1)=0.…(4分)
(2)证明:由(1)知当x>0时恒有f(x)≥0,即x-1≥lnx,
∴ex-1≥x,从而有ex≥x+1,当且仅当x=0时取等号,…(6分)
分别令
 ,
,得
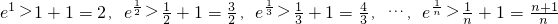 ,
,相乘可得
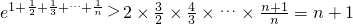 .…(8分)
.…(8分)(3)解:令
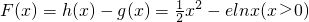 ,
,则
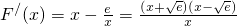 ,
,当
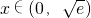 时,F′(x)<0,F(x)递减,
时,F′(x)<0,F(x)递减,当
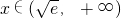 时,F′(x)>0,F(x)递增,
时,F′(x)>0,F(x)递增,∴当
 时F(x)取得最小值0,
时F(x)取得最小值0,则h(x)与g(x)的图象在
 处有公共点
处有公共点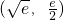 .…(10分)
.…(10分)设函数h(x)与g(x)存在“分界线”,方程为
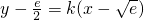 ,
,应有
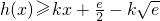 在x∈R时恒成立,
在x∈R时恒成立,即
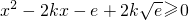 在x∈R时恒成立,
在x∈R时恒成立,必须
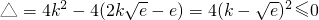 ,
,得
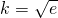 .…(13分)
.…(13分)下证
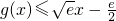 在x>0时恒成立,
在x>0时恒成立,记
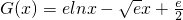 ,
,则
 ,当
,当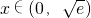 时,G′(x)>0,G(x)递增,
时,G′(x)>0,G(x)递增,当
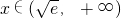 时,G′(x)<0,G(x)递减,
时,G′(x)<0,G(x)递减,∴当
 时G(x)取得最大值0,
时G(x)取得最大值0,即
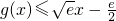 在x>0时恒成立,
在x>0时恒成立,综上知,函数h(x)与g(x)存在“分界线”,其中
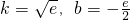 .…(16分)
.…(16分)分析:(1)由f(x)=x-1-lnx(x>0)知
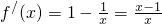 ,当x∈(0,1)时,f′(x)<0,f(x)递减,当x∈(1,+∞)时,f′(x)>0,f(x)递增,由此能求出f(x)的最小值.
,当x∈(0,1)时,f′(x)<0,f(x)递减,当x∈(1,+∞)时,f′(x)>0,f(x)递增,由此能求出f(x)的最小值.(2)由(1)知当x>0时恒有f(x)≥0,即x-1≥lnx,故ex-1≥x,从而有ex≥x+1,当且仅当x=0时取等号,由此能够证明当n∈N*时,
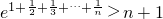 .
.(3)令
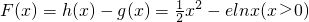 ,则
,则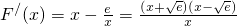 ,当
,当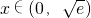 时,F′(x)<0,F(x)递减,当
时,F′(x)<0,F(x)递减,当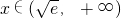 时,F′(x)>0,F(x)递增,故当
时,F′(x)>0,F(x)递增,故当 时F(x)取得最小值0,则h(x)与g(x)的图象在
时F(x)取得最小值0,则h(x)与g(x)的图象在 处有公共点
处有公共点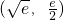 .由此能够导出函数h(x)与g(x)存在“分界线”,其中
.由此能够导出函数h(x)与g(x)存在“分界线”,其中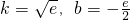 .
.点评:本题考查利用导数求闭区间上函数最值的应用,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|