题目内容
已知不等式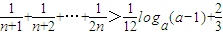
对大于1的自然数n都成立，则实数a的取值范围为 ．
【答案】分析：设Sn=
，（n≥2），由已知，只需
小于Sn的最小值，利用作差法得出Sn随n的增大而增大，当n=2时Sn取得最小值
，再解对数不等式即可．
解答：设Sn=
，（n≥2）则S n+1=
Sn+1-Sn=
=
＞0，∴Sn随n的增大而增大．当n=2时，Sn取得最小值，S2=
∴
恒成立． 移向化简整理得loga（a-1）＜-1．①
根据对数的真数为正得：a-1＞0，a＞1，①再根据对数函数单调性得a-1＜
，a2-a-1＜0，②
①②联立解得
故答案为：
点评：本题是不等式、函数、数列的结合，考查数列的函数性质，对数不等式，分式不等式的解．考查不等式恒成立问题、转化、计算能力．
，（n≥2），由已知，只需小于Sn的最小值，利用作差法得出Sn随n的增大而增大，当n=2时Sn取得最小值，再解对数不等式即可．解答：设Sn=
，（n≥2）则S n+1= Sn+1-Sn=
=＞0，∴Sn随n的增大而增大．当n=2时，Sn取得最小值，S2=∴
恒成立． 移向化简整理得loga（a-1）＜-1．①根据对数的真数为正得：a-1＞0，a＞1，①再根据对数函数单调性得a-1＜
，a2-a-1＜0，②①②联立解得
故答案为：
点评：本题是不等式、函数、数列的结合，考查数列的函数性质，对数不等式，分式不等式的解．考查不等式恒成立问题、转化、计算能力．
练习册系列答案
相关题目
对一切大于1 的整数n都成立，求实数a的取值范围。
对一切大于1的自然数n都成立，则a的取值范围是（ ）
对一切大于1的自然数n都成立，则a的取值范围是 
