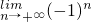摘要:(一)极限 1.数学归纳法是一种用递归方法来证明与正整数有关命题的重要方法.它是完全归纳法中的一种.论证问题分为两步: 证明当n取第一个值时结论正确, 假设当n=k(k∈且k≥)时结论正确.证明当n=k+1时结论也正确. 由断定命题对于从开始的一切正整数都成立. 2.数列极限的定义 设是一个无穷数列.A是一个常数.如果对于预先给定的任意小的正数ε.总存在正整数N.使得只要正整数n>N.就有|-A|<ε.那么就说数列以A为极限.记作=A. 3.数列极限的运算法则 如果=A.=B.那么 (1) (±)=±=A±B, (2) (·)=·=A·B (3) (4)(c·)= c·=cA 极限运算法则中的各个极限都应存在.都可推广到任意有限个极限的情况.不能推广到无限个.在商的运算法则中.要注意对式子的恒等变形.有些题目分母不能直接求极限. 4.特殊数列的极限 (1)C=C = 1(a=l 不存在 (3) =0 (4) (当k=时) = 0(当k<时 不存在(当k>时) 说明:欲求极限的式子中.含有项数与n有关的“和式 或“积式 .应先求和或积. 5.常见的数列极限的类型和求法 (1)“ 型.分子.分母分别求和再转化. (2)“ 型.分子.分母先求和.再化简.转化为有极限. (3)“ 型.将其看作分母为1的分式.转化求极限. 6.与和之间的关系 =a ==a. 如果在点处左.右极限都存在并且等值.则在点处的极限也存在.并且与左.右极限值相同,如果 在处的左.右极限至少有一个不存在.或者左.右极限都存在但不等值.则函数在点处没有极限.这种关系也反映出...也都在处连续.
网址:http://m.1010jiajiao.com/timu_id_4008879[举报]
一个盒子中装有6张卡片,上面分别写着如下6道极限题:
①
;②
;③
;④
;⑤
;⑥
(-1)n
(1)现从盒子中任取两张卡片,求至少有一张卡片上题目极限不存在的概率;
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张记有极取不存在的题的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望. 查看习题详情和答案>>
①
| lim |
| x→∞ |
| 1 |
| x2 |
| lim |
| x→0 |
| 1 |
| x |
| lim |
| x→∞ |
| x2+1 |
| 3x2+x+2 |
| lim |
| x→1 |
| 1 |
| x2-1 |
| lim |
| x→1 |
| x2+x-2 |
| x-1 |
| lim |
| n→+∞ |
(1)现从盒子中任取两张卡片,求至少有一张卡片上题目极限不存在的概率;
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张记有极取不存在的题的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望. 查看习题详情和答案>>
(2012•河南模拟)当前人们普遍认为拓展训练是一种挑战极限、完善人格的训练,某大学生拓展训练中心着眼于大学生的实际情况,精心地设计了三个相互独立的挑战极限项目,并设置了如下计分办法:
据调查,大学生挑战甲项目的成功概率为
,挑战乙项目的成功概率为
,挑战丙项目的成功概率为
.
(1)求某同学三个项目至少一项挑战成功的概率;
(2)记该同学挑战三个项目后所得分数为X,求X的分布列并预测该同学所得分数的数学期望.
查看习题详情和答案>>
| 项目 | 甲 | 乙 | 丙 |
| 挑战成功得分 | 10 | 30 | 60 |
| 挑战失败得分 | 0 | 0 | 0 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 2 |
(1)求某同学三个项目至少一项挑战成功的概率;
(2)记该同学挑战三个项目后所得分数为X,求X的分布列并预测该同学所得分数的数学期望.
当前人们普遍认为拓展训练是一种挑战极限、完善人格的训练,某大学生拓展训练中心着眼于大学生的实际情况,精心地设计了三个相互独立的挑战极限项目,并设置了如下计分办法:
据调查,大学生挑战甲项目的成功概率为 ,挑战乙项目的成功概率为
,挑战乙项目的成功概率为 ,挑战丙项目的成功概率为
,挑战丙项目的成功概率为 .
.
(1)求某同学三个项目至少一项挑战成功的概率;
(2)记该同学挑战三个项目后所得分数为X,求X的分布列并预测该同学所得分数的数学期望.
查看习题详情和答案>>
| 项目 | 甲 | 乙 | 丙 |
| 挑战成功得分 | 10 | 30 | 60 |
| 挑战失败得分 |
 ,挑战乙项目的成功概率为
,挑战乙项目的成功概率为 ,挑战丙项目的成功概率为
,挑战丙项目的成功概率为 .
.(1)求某同学三个项目至少一项挑战成功的概率;
(2)记该同学挑战三个项目后所得分数为X,求X的分布列并预测该同学所得分数的数学期望.
查看习题详情和答案>>
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ;⑥
;⑥
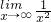 ;②
;②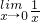 ;③
;③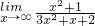 ;④
;④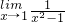 ;⑤
;⑤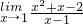 ;⑥
;⑥