摘要： 在几何体ABCDE中.∠BAC=.DC⊥平面ABC.EB⊥平面ABC.F是BC的中点.AB=AC=BE=2.CD=1 (1)求证:DC∥平面ABE, (2)求证:AF⊥平面BCDE, (3)求证:平面AFD⊥平面AFE． 批阅时间 等级 姓名 作业时间: 2010 年 月 日 星期 作业编号 008
网址：http://m.1010jiajiao.com/timu_id_4006237[举报]
在几何体ABCDE中，∠BAC=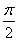
，DC⊥平面ABC，EB⊥平面ABC， AB=AC=BE=2，CD=1。
（1）设平面ABE与平面ACD的交线为直线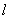
，求证：
∥平面BCDE；
（2）设F是BC的中点，求证：平面AFD⊥平面AFE；
（3）求几何体ABCDE的体积。
查看习题详情和答案>>
在几何体ABCDE中，∠BAC=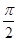
，DC⊥平面ABC，EB⊥平面ABC， AB=AC=BE=2，CD=1。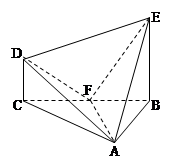
（1）设平面ABE与平面ACD的交线为直线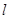
，求证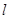：∥平面BCDE；
（2）设F是BC的中点，求证：平面AFD⊥平面AFE；
（3）求几何体ABCDE的体积。
在几何体ABCDE中，∠BAC=
，DC⊥平面ABC，EB⊥平面ABC， AB=AC=BE=2，CD=1.
（1）设平面ABE与平面ACD的交线为直线
，求证：∥平面BCDE；
（2）设F是BC的中点，求证：平面AFD⊥平面AFE；
（3）求几何体ABCDE的体积.
，DC⊥平面ABC，EB⊥平面ABC， AB=AC=BE=2，CD=1.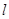
，求证：
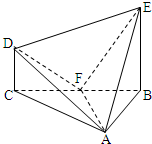在几何体ABCDE中，∠BAC=
，DC⊥平面ABC，EB⊥平面ABC，F是BC的中点，AB=AC=BE=2，CD=1．