题目内容
在几何体ABCDE中,∠BAC=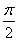 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。

(1)设平面ABE与平面ACD的交线为直线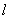 ,求证:
,求证: ∥平面BCDE;
∥平面BCDE;
(2)设F是BC的中点,求证:平面AFD⊥平面AFE;
(3)求几何体ABCDE的体积。
(1)详见解析;(2)详见解析;(3)V=2.
【解析】
试题分析: (1) 由DC⊥平面ABC,EB⊥平面ABC可得DC//EB,从而DC∥平面ABE.再由线面平行的性质定理可得DC∥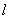 ,又由线面平行的判定定理可得
,又由线面平行的判定定理可得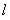 ∥平面BCDE;(2)证面面垂直,首先考虑证哪条线垂直哪个面. 结合题设和图形,可考虑证FD⊥平面AFE.因为在△DEF中,由所给长度及勾股定理可得EF⊥FD.由DC⊥平面ABC可得DC⊥AF,又由AB=AC,F是BC的中点,可得AF⊥BC,从而AF⊥平面BCDE,AF⊥FD.这样由EF⊥FD,AF⊥FD可得FD⊥平面AFE,从而得平面AFD⊥平面AFE.(3)该几何体是一个四棱锥,其顶点为A,底面为BCDE.
∥平面BCDE;(2)证面面垂直,首先考虑证哪条线垂直哪个面. 结合题设和图形,可考虑证FD⊥平面AFE.因为在△DEF中,由所给长度及勾股定理可得EF⊥FD.由DC⊥平面ABC可得DC⊥AF,又由AB=AC,F是BC的中点,可得AF⊥BC,从而AF⊥平面BCDE,AF⊥FD.这样由EF⊥FD,AF⊥FD可得FD⊥平面AFE,从而得平面AFD⊥平面AFE.(3)该几何体是一个四棱锥,其顶点为A,底面为BCDE.
试题解析:(1) ∵DC⊥平面ABC,EB⊥平面ABC
∴DC//EB,又∵DC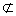 平面ABE,EB
平面ABE,EB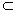 平面ABE,
平面ABE,
∴DC∥平面ABE
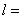 平面ABE
平面ABE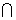 平面ACD,则DC∥
平面ACD,则DC∥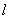
又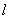
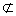 平面BCDE,CD
平面BCDE,CD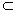 平面BCDE
平面BCDE
所以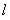 ∥平面BCDE. 4分
∥平面BCDE. 4分
(2)在△DEF中,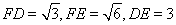 ,由勾股定理知,
,由勾股定理知,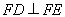
由DC⊥平面ABC,AF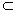 平面ABC,∴DC⊥AF,
平面ABC,∴DC⊥AF,
又∵AB=AC,F是BC的中点,∴AF⊥BC,
又∵DC∩BC=C,DC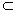 平面BCDE ,BC
平面BCDE ,BC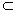 平面BCDE,
平面BCDE,
∴AF⊥平面BCDE,∴AF⊥FD,又∵AF∩FE=F,∴FD⊥平面AFE,
又FD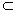 平面AFD,故平面AFD⊥平面AFE. 9分
平面AFD,故平面AFD⊥平面AFE. 9分
(3)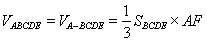 =
= =2. 12分
=2. 12分
考点:1、空间直线与平面的关系;2、几何体的体积.

 阅读快车系列答案
阅读快车系列答案 如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.
如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点. 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC=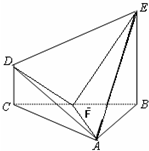 在几何体ABCDE中,
在几何体ABCDE中, 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC=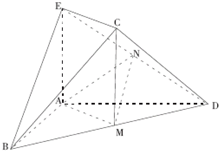 (2013•合肥二模)如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABE.M为线段BD的中点,MC∥AE,AE=MC=
(2013•合肥二模)如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABE.M为线段BD的中点,MC∥AE,AE=MC=