题目内容
 在几何体ABCDE中,∠BAC=
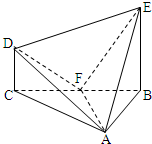
在几何体ABCDE中,∠BAC= ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.
(I)求证:DC∥平面ABE;
(II)求证:AF⊥平面BCDE;
(III)求几何体ABCDE的体积.
(I)证明:∵DC⊥平面ABC,EB⊥平面ABC,∴DC∥EB,
又∵DC?平面ABE,EB?平面ABE,
∴DC∥平面ABE …..(4分)
(II)证明:∵DC⊥平面ABC,AF?平面ABC
∴DC⊥AF,
又∵AB=AC,F是BC的中点,
∴AF⊥BC,
又∵DC∩BC=C,DC?平面BCDE,BC?平面BCDE,
∴AF⊥平面BCDE …..(8分)
(III)解:∵DC⊥平面ABC,EB⊥平面ABC,
∴DC∥EB,且四边形BCDE为直角梯形 …..(9分)
∵在△ABC中,∠BAC= ,AB=AC=2,F是BC的中点
,AB=AC=2,F是BC的中点
∴BC= ,
, …..(11分)
…..(11分)
∵由(II)可知AF⊥平面BCDE
∴几何体ABCDE的体积就是以平面BCDE为底面,AF为高的三棱锥的体积
∴ =
= =2 …..(13分)
=2 …..(13分)
分析:(I)证明DC∥平面ABE,即证DC∥EB,利用DC⊥平面ABC,EB⊥平面ABC可证;
(II)证明AF⊥平面BCDE,利用线面垂直的判定,证明DC⊥AF,AF⊥BC即可;
(III)几何体ABCDE的体积就是以平面BCDE为底面,AF为高的三棱锥的体积.
点评:本题考查线面平行,考查线面垂直,考查几何体的体积,解题的关键是正确线面平行、垂直的判定方法,正确运用体积公式.
又∵DC?平面ABE,EB?平面ABE,
∴DC∥平面ABE …..(4分)
(II)证明:∵DC⊥平面ABC,AF?平面ABC
∴DC⊥AF,
又∵AB=AC,F是BC的中点,
∴AF⊥BC,
又∵DC∩BC=C,DC?平面BCDE,BC?平面BCDE,
∴AF⊥平面BCDE …..(8分)
(III)解:∵DC⊥平面ABC,EB⊥平面ABC,
∴DC∥EB,且四边形BCDE为直角梯形 …..(9分)
∵在△ABC中,∠BAC=
 ,AB=AC=2,F是BC的中点
,AB=AC=2,F是BC的中点∴BC=
 ,
, …..(11分)
…..(11分)∵由(II)可知AF⊥平面BCDE
∴几何体ABCDE的体积就是以平面BCDE为底面,AF为高的三棱锥的体积
∴
 =
= =2 …..(13分)
=2 …..(13分)分析:(I)证明DC∥平面ABE,即证DC∥EB,利用DC⊥平面ABC,EB⊥平面ABC可证;
(II)证明AF⊥平面BCDE,利用线面垂直的判定,证明DC⊥AF,AF⊥BC即可;
(III)几何体ABCDE的体积就是以平面BCDE为底面,AF为高的三棱锥的体积.
点评:本题考查线面平行,考查线面垂直,考查几何体的体积,解题的关键是正确线面平行、垂直的判定方法,正确运用体积公式.

练习册系列答案
相关题目
 如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.
如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点. 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC=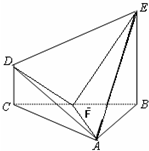 在几何体ABCDE中,
在几何体ABCDE中, 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC=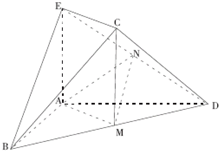 (2013•合肥二模)如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABE.M为线段BD的中点,MC∥AE,AE=MC=
(2013•合肥二模)如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABE.M为线段BD的中点,MC∥AE,AE=MC=