摘要:已知双曲线=1的右焦点是F.右顶点是A,虚轴的上端点是B.·=6-4.∠BAF=150°. (1)求双曲线的方程, (2)设Q是双曲线上的点.且过点F.Q的直线l与y轴交于点M.若+2=0.求直线l的斜率. 解 ,B ·==a(a-c)=6-4 · · cos∠BAF= =-=cos150°=-. ∴a=c,代入a(a-c)=6-4中得c=2. ∴a=,b2=c2-a2=2,故双曲线的方程为. (2)∵点F的坐标为(2.0). ∴可设直线l的方程为y=k(x-2), 令x=0.得y=-2k.即M(0,-2k) 设Q(m,n).则由+2=0得 (m,n+2k)+2(2-m,-n)=(0,0). 即(4-m,2k-n)=(0,0). 即.∵. ∴=1.得k2=.k=±.
网址:http://m.1010jiajiao.com/timu_id_4006019[举报]
已知双曲线![]() =1的右焦点是F,右顶点是A,虚轴的上端点是B,
=1的右焦点是F,右顶点是A,虚轴的上端点是B,![]() ·
·![]() =6-4
=6-4![]() ,∠BAF=150°.
,∠BAF=150°.
(1)求双曲线的方程;
(2)设Q是双曲线上的点,且过点F、Q的直线l与y轴交于点M,若![]() +2
+2![]() =0,求直线l的斜率.
=0,求直线l的斜率.
已知双曲线 =1的右焦点是F,右顶点是A,虚轴的上端点是B,
=1的右焦点是F,右顶点是A,虚轴的上端点是B, =6
=6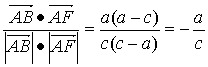 ,∠BAF=150°.
,∠BAF=150°.
(Ⅰ)求双曲线的方程;
(Ⅱ)设Q是双曲线上的一点,且过点F、Q的直线l与y轴交于点M,若![]() =0,求直线l的斜率.
=0,求直线l的斜率.
已知双曲线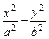 =1的右焦点是F,右顶点是A,虚轴的上端点是B,
=1的右焦点是F,右顶点是A,虚轴的上端点是B,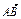 ·
·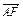 =6-4
=6-4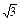 ,∠BAF=150°.
,∠BAF=150°.
(1)求双曲线的方程;
(2)设Q是双曲线上的点,且过点F、Q的直线l与y轴交于点M,若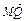 +2
+2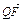 =0,求直线l的斜率.
=0,求直线l的斜率.
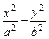 =1的右焦点是F,右顶点是A,虚轴的上端点是B,
=1的右焦点是F,右顶点是A,虚轴的上端点是B,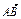 ·
·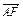 =6-4
=6-4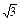 ,∠BAF=150°.
,∠BAF=150°.(1)求双曲线的方程;
(2)设Q是双曲线上的点,且过点F、Q的直线l与y轴交于点M,若
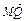 +2
+2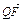 =0,求直线l的斜率.
=0,求直线l的斜率.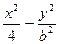 ="1"
="1" 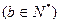 的两个焦点为
的两个焦点为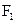 、
、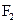 ,P是双曲线上的一点,
,P是双曲线上的一点,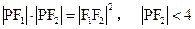 ,
,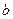 的值;
的值;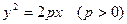 的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.
的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.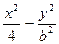 ="1"
="1" 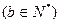 的两个焦点为
的两个焦点为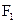 、
、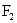 ,P是双曲线上的一点,
,P是双曲线上的一点,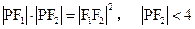 ,
,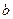 的值;
的值;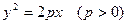 的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.
的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.