题目内容
已知双曲线(Ⅰ)求双曲线的方程;
(Ⅱ)设Q是双曲线上的一点,且过点F、Q的直线l与y轴交于点M,若![]() =0,求直线l的斜率.
=0,求直线l的斜率.
解:(Ⅰ)由条件知A(a,0),B(0,b),F(c,0).
![]() =(-a,b)·(c-a,0)=a(a-c)=6-
=(-a,b)·(c-a,0)=a(a-c)=6-![]() ,
,
cos∠BAF=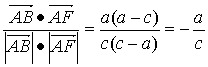 =cos150°=-
=cos150°=-![]() ,∴a=
,∴a=![]() c,
c,
代入a(a-c)=6-![]() 中得c=
中得c=![]() ,∴a=
,∴a=![]() ,b2=c2-a2=2.故双曲线的方程为
,b2=c2-a2=2.故双曲线的方程为![]() =1.
=1.
(Ⅱ)∵点F的坐标为(![]() ,0),∴可设直线l的方程为y=k(x-
,0),∴可设直线l的方程为y=k(x-![]() ),令x=0,得y=-
),令x=0,得y=-![]() k,即M(0,-
k,即M(0,-![]() k).
k).
设Q(m,n),,则![]() =0得(m,n+
=0得(m,n+![]() k)+2(
k)+2(![]() -m,-n)=(0,0),
-m,-n)=(0,0),
即(![]() -m,
-m,![]() k-n)=(0,0),
k-n)=(0,0),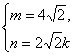 .
.
∵![]() =1,∴
=1,∴![]() =1,得k2=
=1,得k2=![]() ,k=±
,k=±![]() .
.
故直线l的斜率为±![]() .
.

练习册系列答案
相关题目
 的方程为
的方程为  ,双曲线
,双曲线 的左、右焦
的左、右焦 与双曲线C2恒有两个不同的交点A和B,求
与双曲线C2恒有两个不同的交点A和B,求 的范围。
的范围。