题目内容
已知双曲线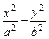 =1的右焦点是F,右顶点是A,虚轴的上端点是B,
=1的右焦点是F,右顶点是A,虚轴的上端点是B,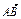 ·
·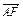 =6-4
=6-4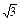 ,∠BAF=150°.
,∠BAF=150°.
(1)求双曲线的方程;
(2)设Q是双曲线上的点,且过点F、Q的直线l与y轴交于点M,若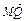 +2
+2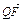 =0,求直线l的斜率.
=0,求直线l的斜率.
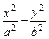 =1的右焦点是F,右顶点是A,虚轴的上端点是B,
=1的右焦点是F,右顶点是A,虚轴的上端点是B,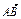 ·
·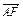 =6-4
=6-4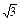 ,∠BAF=150°.
,∠BAF=150°.(1)求双曲线的方程;
(2)设Q是双曲线上的点,且过点F、Q的直线l与y轴交于点M,若
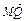 +2
+2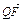 =0,求直线l的斜率.
=0,求直线l的斜率.(1) (2)k=±
(2)k=±
 (2)k=±
(2)k=±
(1)由条件知A(a,0),B(0,b),F(c,0)
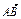 ·
·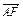 =(-a, b)·(c-a,0)=a(a-c)=6-4
=(-a, b)·(c-a,0)=a(a-c)=6-4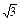
cos∠BAF= =-
=- =cos150°=-
=cos150°=- .
.
∴a= c,代入a(a-c)=6-4
c,代入a(a-c)=6-4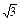 中得c=2
中得c=2 .
.
∴a= ,b2=c2-a2=2,故双曲线的方程为
,b2=c2-a2=2,故双曲线的方程为 .
.
(2)∵点F的坐标为(2 ,0).
,0).
∴可设直线l的方程为y=k(x-2 ),
),
令x=0,得y=-2 k,即M(0,-2
k,即M(0,-2 k)
k)
设Q(m,n),则由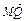 +2
+2 =0得
=0得
(m,n+2 k)+2(2
k)+2(2 -m,-n)=(0,0).
-m,-n)=(0,0).
即(4 -m,2
-m,2 k-n)=(0,0).
k-n)=(0,0).
即 ,∵
,∵ .
.
∴ =1,得k2=
=1,得k2= ,k=±
,k=± .
.
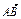 ·
·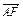 =(-a, b)·(c-a,0)=a(a-c)=6-4
=(-a, b)·(c-a,0)=a(a-c)=6-4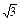
|
|
 =-
=- =cos150°=-
=cos150°=- .
.∴a=
 c,代入a(a-c)=6-4
c,代入a(a-c)=6-4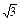 中得c=2
中得c=2 .
.∴a=
 ,b2=c2-a2=2,故双曲线的方程为
,b2=c2-a2=2,故双曲线的方程为 .
.(2)∵点F的坐标为(2
 ,0).
,0).∴可设直线l的方程为y=k(x-2
 ),
),令x=0,得y=-2
 k,即M(0,-2
k,即M(0,-2 k)
k)设Q(m,n),则由
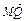 +2
+2 =0得
=0得(m,n+2
 k)+2(2
k)+2(2 -m,-n)=(0,0).
-m,-n)=(0,0).即(4
 -m,2
-m,2 k-n)=(0,0).
k-n)=(0,0).即
 ,∵
,∵ .
.∴
 =1,得k2=
=1,得k2= ,k=±
,k=± .
.
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
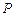 的轨迹是曲线
的轨迹是曲线 ,满足点
,满足点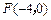 的距离与它到直线
的距离与它到直线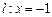 的距离
的距离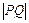 之比为常数,又点
之比为常数,又点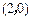 在曲线
在曲线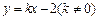 与曲线
与曲线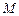 和
和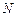 ,求实数
,求实数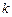 的取值范围.
的取值范围.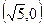 和曲线
和曲线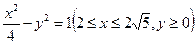 上的点
上的点 …、
…、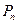 。若
。若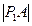 、
、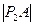 、…、
、…、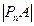 成等差数列且公差d >0,(1). 试将d表示为n的函数关系式.(2). 若
成等差数列且公差d >0,(1). 试将d表示为n的函数关系式.(2). 若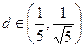 ,是否存在满足条件的
,是否存在满足条件的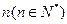 .若存在,求出n可取的所有值,若不存在,说明理由.
.若存在,求出n可取的所有值,若不存在,说明理由.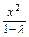 -
-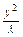 =1(0<
=1(0<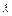 <1)的右焦点为B,过点B作直线交双曲线C的右支于M、N两点,试确定
<1)的右焦点为B,过点B作直线交双曲线C的右支于M、N两点,试确定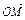 ·
·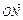 =0,其中点O为坐标原点.
=0,其中点O为坐标原点.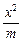 +
+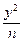 =1(m>n>0)和双曲线
=1(m>n>0)和双曲线 -
-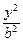 =1(a>b>0)有相同的焦点F1、F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是
=1(a>b>0)有相同的焦点F1、F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是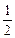 (m-a)
(m-a)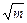 -
-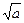
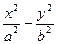 =1的右焦点,斜率k=2,若l与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率e的取值范围是( )
=1的右焦点,斜率k=2,若l与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率e的取值范围是( )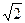
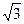
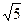
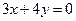 ,一焦点为(4,0)的双曲线标准方程是
,一焦点为(4,0)的双曲线标准方程是 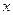 、
、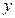 满足条件
满足条件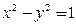 ,则
,则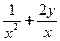 的取值范围是___________________.
的取值范围是___________________.