摘要: 趋向于定值的函数极限概念:当自变量无限趋近于()时.如果函数无限趋近于一个常数.就说当趋向时.函数的极限是.记作特别地.,
网址:http://m.1010jiajiao.com/timu_id_4001745[举报]
在周长为定值的△ABC中,已知|AB|=2
,动点C的运动轨迹为曲线G,且当动点C运动时,cosC有最小值-
.
(1)以AB所在直线为x轴,线段AB的中垂线为y轴建立直角坐标系,求曲线G的方程.
(2)过点(m,0)作圆x2+y2=1的切线l交曲线G于M,N两点.将线段MN的长|MN|表示为m的函数 ,并求|MN|的最大值.
查看习题详情和答案>>
| 3 |
| 1 |
| 2 |
(1)以AB所在直线为x轴,线段AB的中垂线为y轴建立直角坐标系,求曲线G的方程.
(2)过点(m,0)作圆x2+y2=1的切线l交曲线G于M,N两点.将线段MN的长|MN|表示为m的函数
(本小题满分14分)在周长为定值的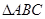 中,已知
中,已知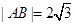 ,动点
,动点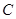 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点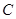 运动时,
运动时,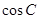 有最小值
有最小值 .
.
(1)以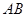 所在直线为
所在直线为 轴,线段
轴,线段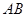 的中垂线为
的中垂线为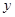 轴建立直角坐标系,求曲线G的方程.
轴建立直角坐标系,求曲线G的方程.
(2)过点(m,0)作圆x2+y2=1的切线l交曲线G于M,N两点.将线段MN的长|MN|表示为m的函数,并求|MN|的最大值.
查看习题详情和答案>>
(本小题满分14分)在周长为定值的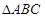 中,已知
中,已知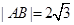 ,动点
,动点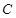 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点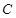 运动时,
运动时,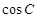 有最小值
有最小值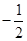 .
.
(1) 以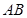 所在直线为
所在直线为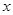 轴,线段
轴,线段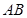 的中垂线为
的中垂线为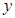 轴建立直角坐标系,求曲线
轴建立直角坐标系,求曲线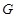 的方程;
的方程;
(2) 过点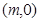 作圆
作圆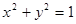 的切线
的切线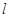 交曲线
交曲线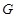 于
于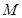 ,
,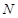 两点.将线段MN的长|MN|表示为
两点.将线段MN的长|MN|表示为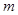 的函数,并求|MN|的最大值.
的函数,并求|MN|的最大值.
查看习题详情和答案>>
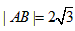 ,动点C的运动轨迹为曲线G,且当动点C运动时,cosC有最小值
,动点C的运动轨迹为曲线G,且当动点C运动时,cosC有最小值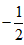 。
。