题目内容
在周长为定值的![]() 中,已知
中,已知![]() ,动点
,动点![]() 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点![]() 运动时,
运动时,![]() 有最小值
有最小值![]() .
.
(1)以![]() 所在直线为
所在直线为![]() 轴,线段
轴,线段![]() 的中垂线为
的中垂线为![]() 轴建立直角坐标系,求曲线G的方程.
轴建立直角坐标系,求曲线G的方程.
(2)过点(m,0)作圆x2+y2=1的切线l交曲线G于M,N两点.将线段MN的长|MN|表示为m的函数,并求|MN|的最大值.
解:(1)设 ![]() (
(![]() )为定值,所以C点的轨迹是以A、B为焦点的椭圆,所以焦距
)为定值,所以C点的轨迹是以A、B为焦点的椭圆,所以焦距![]() . (2分)
. (2分)
因为
![]()
又 ![]() ,所以
,所以 ![]() ,由题意得
,由题意得 ![]() .
.
所以C点轨迹G 的方程为 ![]() (6分)
(6分)
(2) .由题意知,|m|≥1.
当m=1时,切线l的方程为x=1,点M,N的坐标分别为![]() ,
,![]() ,此时|MN|=
,此时|MN|=![]() .
.
当m=-1时,同理可知|MN|=![]() . (7分)
. (7分)
当|m|>1时,设切线l的方程为y=k(x-m),
由 得(1+4k2)x2-8k2mx+4k2m2-4=0. (8分)
得(1+4k2)x2-8k2mx+4k2m2-4=0. (8分)
设M,N两点的坐标分别为(x1,y1),(x2,y2),
则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
又由l与圆x2+y2=1相切,得![]() =1,即m2k2=k2+1,
=1,即m2k2=k2+1,
所以|MN|=![]() =
=![]()
=  =
=![]() . (12分)
. (12分)
由于当m=±1时,|MN|=![]() .
.
所以|MN|=![]() ,m∈(-∞,-1 ]∪[1,+∞).
,m∈(-∞,-1 ]∪[1,+∞).
因为|MN|=![]() =
= ≤2,且当m=±
≤2,且当m=±![]() 时,|MN|=2.
时,|MN|=2.
所以|MN|的最大值为2. (14分)

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
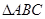 中,已知
中,已知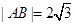 ,动点
,动点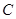 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点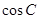 有最小值
有最小值 .
.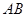 所在直线为
所在直线为 轴,线段
轴,线段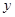 轴建立直角坐标系,求曲线G的方程.
轴建立直角坐标系,求曲线G的方程. 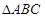 中,已知
中,已知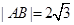 ,动点
,动点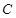 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点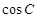 有最小值
有最小值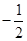 .
.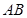 所在直线为
所在直线为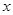 轴,线段
轴,线段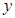 轴建立直角坐标系,求曲线
轴建立直角坐标系,求曲线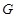 的方程;
的方程;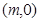 作圆
作圆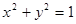 的切线
的切线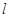 交曲线
交曲线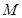 ,
,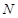 两点.将线段MN的长|MN|表示为
两点.将线段MN的长|MN|表示为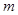 的函数,并求|MN|的最大值.
的函数,并求|MN|的最大值.