题目内容
三个同学对问题“关于x的不等式x2+25+|x3-5x2|≥ax在[1,12]上恒成立,求实数a的取值范围”提出各自的解题思路.甲说:“只需不等式左边的最小值不小于右边的最大值.”
乙说:“把不等式变形为左边含变量x的函数,右边仅含常数,求函数的最值.”
丙说:“把不等式两边看成关于x的函数,作出函数图象.”
参考上述解题思路,你认为他们所讨论的问题的正确结论,即a的取值范围是__________.
a≤10
解析:由x2+25+|x3-5x2|≥ax,x∈[1,12],变形为a≤x+![]() +|x2-5x|.设f(x)=x+
+|x2-5x|.设f(x)=x+![]() +|x2-5x|.
+|x2-5x|.
∵x+![]() ≥
≥![]() =10,此时x=5.又x=5时,|x2-5x|=0,
=10,此时x=5.又x=5时,|x2-5x|=0,
∴f(x)的最小值为10.∴a≤10,x∈[1,12]成立.

练习册系列答案
相关题目
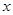 的不等式
的不等式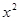 +25+|
+25+|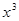 -5
-5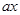 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数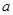 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路. 的不等式
的不等式 +25+|
+25+| -5
-5 在[1,12]上恒成
在[1,12]上恒成 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.