摘要:11.如图.点A(a,0)在x轴上(a>0).点B在y轴上.以AB为一边作正△ABC.点B在y轴上移动时.求点C的轨迹的极坐标方程. 解:以A为极点.射线Ax为极轴建系.则y轴的极坐标方程为 ρcosθ=-a. 设C(ρ.θ).B(ρ0.θ0). ∵△ABC为正三角形. ∴|CA|=|BA|. 即ρ=ρ0.θ0=θ+. 又∵ρ0cosθ0=-a. ∴ρcos(θ+)=-a.这就是点C的轨迹方程.
网址:http://m.1010jiajiao.com/timu_id_3971647[举报]
 如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方,
如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方,| PA |
| PF |
(Ⅰ)求椭圆的方程和离心率;
(Ⅱ)求点P的坐标;
(Ⅲ)若过点F且倾斜角为45°的直线l交椭圆于D,E两点,求△ADE的面积.
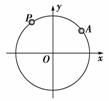
如图,点A在半径为1且圆心在原点的圆上,且∠AOx=45°.点P
从点A出发,依逆时针方向等速地沿单位圆周旋转.已知P在1秒钟内转过的角度为θ(0°<θ<180°),经过2秒钟到达第三象限,经过14秒钟后又回到出发点A,求θ.
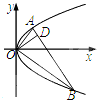 如图,点A,B在抛物线y2=2px(p>0)上,且OA⊥OB,OD⊥AB交AB于D,则点D在( )
如图,点A,B在抛物线y2=2px(p>0)上,且OA⊥OB,OD⊥AB交AB于D,则点D在( ) .
.
