题目内容
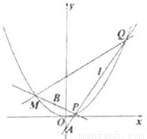
如图,过点A(-1,0),斜率为k的直线l与抛物线C:y2=4x交于P、Q两点.若曲线C的焦点F与P、Q、R三点按如图顺序构成平行四边形PFQR,求点R的轨迹方程.
解:由已知l:y=k(x+1),
消x得![]() y2-y+k=0.?
y2-y+k=0.?
∵直线l交C于两点P、Q,?
∴ 解得-1<k<0或0<k<1.?
解得-1<k<0或0<k<1.?
设P(x1,y1)、Q(x2,y2)、R(x,y),M是PQ中点,如图:?

∵y1+y2=![]() ,∴M点纵坐标yM
,∴M点纵坐标yM![]() ,将其代入l方程,得xM
,将其代入l方程,得xM![]() =-1.?
=-1.?
∵PFQR是平行四边行,?
∴R、F中点也是M,而F(1,0),?
∴x=![]() -3,y=
-3,y=![]() ,消k得y2=4(x+3).?
,消k得y2=4(x+3).?
又∵k∈(-1,0)∪(0,1),∴x∈(1,+∞),?
∴点R的轨迹方程为y2=4(x+3)(x>1).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•温州一模)如图,过点A(0,-1)的动直线l与抛物线C:x2=4y交于P(x1,y1),Q(x2,y2)两点.
(2012•温州一模)如图,过点A(0,-1)的动直线l与抛物线C:x2=4y交于P(x1,y1),Q(x2,y2)两点.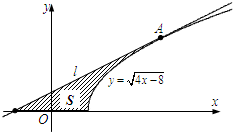 (2008•盐城一模)如图,过点A(6,4)作曲线f(x)=
(2008•盐城一模)如图,过点A(6,4)作曲线f(x)=