题目内容
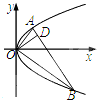 如图,点A,B在抛物线y2=2px(p>0)上,且OA⊥OB,OD⊥AB交AB于D,则点D在( )
如图,点A,B在抛物线y2=2px(p>0)上,且OA⊥OB,OD⊥AB交AB于D,则点D在( )分析:设出A,B,D的坐标,利用OA⊥OB,可得y1y2=-4p2,利用OD⊥AB,A,D,B共线,即可求得结论.
解答:解:设A(x1,y1),B(x2,y2),D(x,y),(y1≠y2)则
∵OA⊥OB,∴x1x2+y1y2=0
∵点A,B在抛物线y2=2px
∴y12y22=4p2x1x2,
∴y1y2=-4p2,
∵OD⊥AB,∴
•
=-1
∴
•
=-1
∵A,D,B共线,
=(x-x1,y-y1),
=(x-x2,y-y2)
∴(x-x1)(y-y2)=(y-y1)(x-x2)
∴x•(y1-y2)+y•
+
=0
∴x-y•
-2p=0
∴x-y•(-
)-2p=0
∴x2+y2-2px=0,(x≠0).
即D点的轨迹方程为x2+y2-2px=0,(x≠0).
故选D.
∵OA⊥OB,∴x1x2+y1y2=0
∵点A,B在抛物线y2=2px
∴y12y22=4p2x1x2,
∴y1y2=-4p2,
∵OD⊥AB,∴
| y |
| x |
| y2-y1 |
| x2-x1 |
∴
| y |
| x |
| 2p |
| y2+y1 |
∵A,D,B共线,
| AD |
| BD |
∴(x-x1)(y-y2)=(y-y1)(x-x2)
∴x•(y1-y2)+y•
| y22-y12 |
| 2p |
| y1y2(y1-y2) |
| 2p |
∴x-y•
| y1+y2 |
| 2p |
∴x-y•(-
| y |
| x |
∴x2+y2-2px=0,(x≠0).
即D点的轨迹方程为x2+y2-2px=0,(x≠0).
故选D.
点评:本题考查点的轨迹方程的求法,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆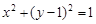 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
 且
且 交于点M,求
交于点M,求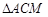 与
与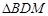 面积之和的最小值.
面积之和的最小值.
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 |BD|为定值;
|BD|为定值;
