摘要:18. 已知动圆过定点F(0,2).且与定直线L:y=-2相切. (1)求动圆圆心的轨迹C的方程, (2)若AB是轨迹C的动弦.且AB过F(0,2).分别以A.B为切点作轨迹C的切线.设两切线交点为Q.证明:AQ⊥BQ. 解:(1)依题意.圆心的轨迹是以F(0,2)为焦点.L:y=-2为准线的抛物线. 因为抛物线焦点到准线距离等于4. 所以圆心的轨迹是x2=8y. (2)证明:因为直线AB与x轴不垂直. 设AB:y=kx+2. A(x1.y1).B(x2.y2). 由 可得x2-8kx-16=0.x1+x2=8k.x1x2=-16. 抛物线方程为y=x2.求导得y′=x. 所以过抛物线上A.B两点的切线斜率分别是k1=x1.k2=x2.k1k2=x1·x2=x1·x2=-1. 所以AQ⊥BQ.
网址:http://m.1010jiajiao.com/timu_id_3971518[举报]
(2010•唐山二模)A、B是椭圆x2+
=1上的点,O为原点,OA与OB斜率的乘积等于-2,
=
+
.
(I)求证:点C在另一个椭圆上;
(II)求四边形OACB的面积.
查看习题详情和答案>>
| y2 |
| 2 |
| OC |
| OA |
| OB |
(I)求证:点C在另一个椭圆上;
(II)求四边形OACB的面积.
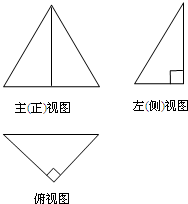 (2010•深圳二模)如图,是一个空间几何体的三视图,其主(正)视图是一个边长为2的正三角形,俯视图是一个斜边为2的等腰直角三角形,左(侧)视图是一个两直角边分别为
(2010•深圳二模)如图,是一个空间几何体的三视图,其主(正)视图是一个边长为2的正三角形,俯视图是一个斜边为2的等腰直角三角形,左(侧)视图是一个两直角边分别为| 3 |
 (2010•和平区一模)如图,在直三棱柱ABC-A1B1C1中,已知AA1=2,AC=BC=1,且AC⊥BC,M是A1B1的中点.
(2010•和平区一模)如图,在直三棱柱ABC-A1B1C1中,已知AA1=2,AC=BC=1,且AC⊥BC,M是A1B1的中点.