摘要:14.已知数列满足.对于所有正整数.有.求使得成立的最小正整数. 解法一 设.的特征方程为.特征根为.结合.得.由二项式定理得. 当为奇数时., 当为偶数时.. 于是.即.所以满足条件的最小正整数为. 解法二 下面都是在模意义下的,则,即,因此数列在模意义下具有等差数列的特点.又因为.所以.于是有.因此满足条件的最小正整数为.
网址:http://m.1010jiajiao.com/timu_id_3963738[举报]
已知数列![]() 满足:
满足:![]() ,我们把使a1· a2·…·ak为整数的数k(
,我们把使a1· a2·…·ak为整数的数k(![]() )叫做数列
)叫做数列![]() 的理想数,给出下列关于数列
的理想数,给出下列关于数列![]() 的几个结论:①数列
的几个结论:①数列![]() 的最小理想数是2;②数列
的最小理想数是2;②数列![]() 的理想数k的形式可以表示为
的理想数k的形式可以表示为![]() ;③在区间(1,1000)内数列
;③在区间(1,1000)内数列![]() 的所有理想数之和为1004;④对任意
的所有理想数之和为1004;④对任意![]() ,有
,有![]() >
>![]() 。其中正确结论的序号为 。
。其中正确结论的序号为 。
 中,
中, ,且有
,且有 .
. 所有可能的值;
所有可能的值; ,都有
,都有 成立?若有,请写出这个数列的前6项,若没有,说明理由;
成立?若有,请写出这个数列的前6项,若没有,说明理由; 的最小值.
的最小值.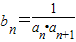 .
.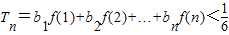 (n≥1);
(n≥1); (a>0),求同时满足下列两个条件的所有a的值:①对于任意正整数n,都有
(a>0),求同时满足下列两个条件的所有a的值:①对于任意正整数n,都有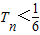 ;②对于任意的
;②对于任意的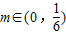 ,均存在n∈N*,使得n≥n时,Tn>m.
,均存在n∈N*,使得n≥n时,Tn>m.