Question

已知数列{a_n}中，a₁=3，a₂=5，其前n项和S_n满足S_n+S_n-2=2S_n-1+2^n-1（n≥3）．令．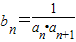
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）若f（x）=2^x-1，求证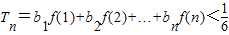：（n≥1）；
（Ⅲ）令（a＞0），求同时满足下列两个条件的所有a的值：①对于任意正整数n，都有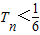；②对于任意的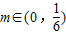，均存在n∈N^*，使得n≥n时，T_n＞m．

Answer 1

【答案】分析：（Ⅰ）由题意知S_n-S_n-1=S_n-1-S_n-2+2^n-1（n≥3）即a_n=a_n-1+2^n-1再用累加法求解．
（Ⅱ）由（I）求得b_n，再观察T_n=b₁f（1）+b₂f（2）+…+b_nf（n）可用裂项相消法求解．
（Ⅲ）受（II ）的启发，我们可以先a=2研究，由（Ⅱ）知：，即条件①满足；又，
∴．
因为是恒成立，所以取n等于不超过的最大整数，则当n≥n时，T_n＞m（ⅱ）当a＞2时，∵n≥1，，∴，．（ⅲ）当0＜a＜2时，∵n≥1，，∴，分别放缩研究．
解答：解：（Ⅰ）由题意知S_n-S_n-1=S_n-1-S_n-2+2^n-1（n≥3）
即a_n=a_n-1+2^n-1（n≥3）（1分）
∴a_n=（a_n-a_n-1）+（a_n-1-a_n-2）++（a₃-a₂）+a₂
=2^n-1+2^n-2++2²+5
=2^n-1+2^n-2++2²+2+1+2
=2ⁿ+1（n≥3）（3分）
检验知n=1、2时，结论也成立，故a_n=2ⁿ+1．（4分）
（Ⅱ）由于
故
=．（9分）
（Ⅲ）（ⅰ）当a=2时，由（Ⅱ）知：，即条件①满足；又，
∴．
取n等于不超过的最大整数，则当n≥n时，T_n＞m．（10分）
（ⅱ）当a＞2时，∵n≥1，，∴，
∴．
∴．
由（ⅰ）知存在n∈N^*，当n≥n时，，
故存在n∈N^*，当n≥n时，，不满足条件．（12分）
（ⅲ）当0＜a＜2时，∵n≥1，，∴，
∴．
∴．
取，若存在n∈N^*，当n≥n时，T_n＞m，
则．
∴矛盾．故不存在n∈N^*，
当n≥n时，T_n＞m．不满足条件．
综上所述：只有a=2时满足条件，故a=2．（14分）
点评：本题主要考查累加法求通项，裂项相消法求和，具体到一般分类讨论等思想方法的运用．