摘要:设向量..其中s,t为不同时为0的两个实数.实数.满足. (1)求函数关系S=F; (2) 若F在上单调递增.求实数的取值范围, (3)对于上述F.当=0时.存在正数列{n},满足F+F+--+F=².其中.求证: 雅安中学09-10学年高二上学期九月月考
网址:http://m.1010jiajiao.com/timu_id_3956251[举报]
设向量![]() ,
,![]() ,其中s,t为不同时为0的两个实数,实数
,其中s,t为不同时为0的两个实数,实数![]() ,满足
,满足![]() 。
。
(1)求函数关系S=F![]() ;
;
(2) 若F![]() 在(1,+∞)上单调递增,求实数
在(1,+∞)上单调递增,求实数![]() 的取值范围;
的取值范围;
(3)对于上述F![]() ,当
,当![]() =0时,存在正数列{
=0时,存在正数列{![]() n},满足F
n},满足F![]() +F
+F![]() +……+F
+……+F![]() =
=![]() ²,其中
²,其中![]() ,求证:
,求证:![]()
设向量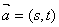 ,
,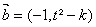 ,其中s,t为不同时为0的两个实数,实数
,其中s,t为不同时为0的两个实数,实数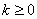 ,满足
,满足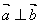 。
。
(1)求函数关系S=F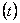 ;
;
(2) 若F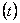 在(1,+∞)上单调递增,求实数
在(1,+∞)上单调递增,求实数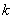 的取值范围;
的取值范围;
(3)对于上述F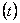 ,当
,当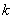 =0时,存在正数列{
=0时,存在正数列{ n},满足F
n},满足F +F
+F +……+F
+……+F =
=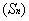 ²,其中
²,其中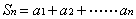 ,求证:
,求证:
查看习题详情和答案>>
设平面上的动向量![]() ,
,![]() ,其中s、t为不同时为0的两个实数,实数
,其中s、t为不同时为0的两个实数,实数![]() ,满足
,满足![]() 。
。
(1)求函数关系式![]() ;
;
(2)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的范围;
的范围;
(3)对上述![]() ,当
,当![]() 时,存在正项数列
时,存在正项数列![]() 满足
满足![]() ,其中
,其中![]() ,证明:
,证明: 。
。