题目内容
设向量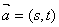 ,
,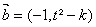 ,其中s,t为不同时为0的两个实数,实数
,其中s,t为不同时为0的两个实数,实数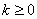 ,满足
,满足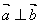 。
。
(1)求函数关系S=F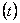 ;
;
(2) 若F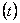 在(1,+∞)上单调递增,求实数
在(1,+∞)上单调递增,求实数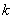 的取值范围;
的取值范围;
(3)对于上述F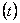 ,当
,当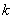 =0时,存在正数列{
=0时,存在正数列{ n},满足F
n},满足F +F
+F +……+F
+……+F =
=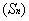 ²,其中
²,其中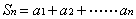 ,求证:
,求证:
【答案】
解:(1)因为 ,所以
,所以
即 ³
³
(2)在(1,+∞)任意取1<t1<t2,因为函数F(t)在定义域内递增

即 成立
成立

(3) 

 =
=
 又
又

 =
= 两式相减
两式相减
得 
再由 两式相减
两式相减
得 ,所以数列{
,所以数列{ }是公差为1的等差数列。
}是公差为1的等差数列。
又 ,得
,得

又



 =
= =
=



练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,
, ,且
,且 的模分别为s,t,其中s=
的模分别为s,t,其中s= =1,t=
=1,t= ,
, 则
则 的模为__
_
的模为__
_ 。
。