摘要: 已知焦点在轴上的椭圆上存在两点.关于直线对称.求的取值范围. 解法1:如图8-6.由题意可设.两点所在直线方程设为. 代入椭圆方程得 . 由 得 . 设.则 . . 所以的中点. 因为点在直线上. 所以. 解得.再将代入得 . 解得或. 因为 . 所以. 解法2:设..中点. 由题意可得 由③-④得. 将①②代入得. 将⑤代入结果得. 再将⑥代入得. 解得..将.代入⑦得 . 化简得. 解得或. 因为 . 所以. 点评:对称问题应注意运用以下结论建立关系式: (1)对称点的连线与对称轴垂直, (2)对称点的中点在对称轴上, (3)对称点所在的直线与曲线相交于两个不同的点. 本题在求参数范围时.解法1是利用构造含参数的不等式.解法2是利用的中点在椭圆内构造含参数的不等式.
网址:http://m.1010jiajiao.com/timu_id_3938377[举报]
已知焦点在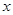 轴上的椭圆
轴上的椭圆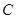 过点
过点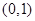 ,且离心率为
,且离心率为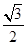 ,
,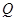 为椭圆
为椭圆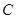 的左顶点.
的左顶点.
(1)求椭圆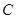 的标准方程;
的标准方程;
(2)已知过点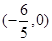 的直线
的直线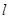 与椭圆
与椭圆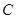 交于
交于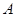 ,
,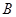 两点.
两点.
(ⅰ)若直线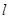 垂直于
垂直于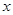 轴,求
轴,求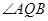 的大小;
的大小;
(ⅱ)若直线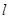 与
与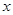 轴不垂直,是否存在直线
轴不垂直,是否存在直线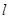 使得
使得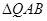 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线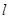 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
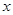 轴上的椭圆
轴上的椭圆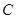 过点
过点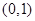 ,且离心率为
,且离心率为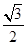 ,
,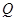 为椭圆
为椭圆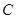 的左顶点.
的左顶点.(1)求椭圆
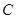 的标准方程;
的标准方程;(2)已知过点
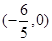 的直线
的直线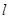 与椭圆
与椭圆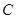 交于
交于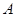 ,
,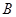 两点.
两点.(ⅰ)若直线
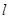 垂直于
垂直于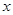 轴,求
轴,求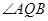 的大小;
的大小;(ⅱ)若直线
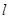 与
与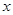 轴不垂直,是否存在直线
轴不垂直,是否存在直线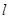 使得
使得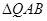 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线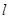 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 的左顶点.
的左顶点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(ⅰ)若直线![]() 垂直于
垂直于![]() 轴,求
轴,求![]() 的大小;
的大小;
(ⅱ)若直线![]() 与
与![]() 轴不垂直,是否存在直线
轴不垂直,是否存在直线![]() 使得
使得![]() 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
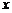 轴上的椭圆
轴上的椭圆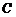 过点
过点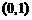 ,且离心率为
,且离心率为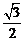 ,
,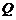 为椭圆
为椭圆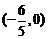 的直线
的直线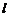 与椭圆
与椭圆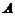 ,
,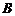 两点.
两点.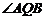 的大小;
的大小; 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线 已知焦点在x轴上的椭圆C过点(0,1),且离心率为
已知焦点在x轴上的椭圆C过点(0,1),且离心率为 ,Q为椭圆C的左顶点.
,Q为椭圆C的左顶点.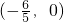 的直线l与椭圆C交于A,B两点.
的直线l与椭圆C交于A,B两点.