题目内容
已知焦点在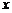 轴上的椭圆
轴上的椭圆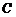 过点
过点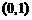 ,且离心率为
,且离心率为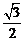 ,
,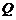 为椭圆
为椭圆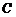 的左顶点.
的左顶点.
(Ⅰ)求椭圆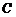 的标准方程;
的标准方程;
(Ⅱ)已知过点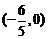 的直线
的直线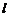 与椭圆
与椭圆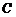 交于
交于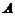 ,
,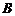 两点.
两点.
(ⅰ)若直线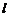 垂直于
垂直于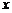 轴,求
轴,求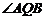 的大小;
的大小;
(ⅱ)若直线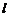 与
与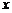 轴不垂直,是否存在直线
轴不垂直,是否存在直线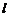 使得
使得 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线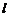 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
【答案】
(Ⅰ)设椭圆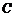 的标准方程为
的标准方程为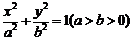 ,且
,且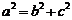 .
.
由题意可知: ,
,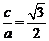 . ………2分
. ………2分
所以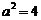 .
.
所以,椭圆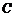 的标准方程为
的标准方程为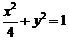 . ………3分
. ………3分
(Ⅱ)由(Ⅰ)得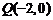 .设
.设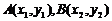 .
.
(ⅰ)当直线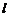 垂直于
垂直于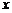 轴时,直线
轴时,直线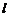 的方程为
的方程为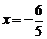 .
.
由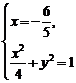 解得:
解得: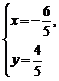 或
或
即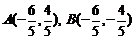 (不妨设点
(不妨设点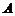 在
在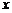 轴上方).…………5分
轴上方).…………5分
则直线 的斜率
的斜率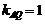 ,直线
,直线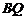 的斜率
的斜率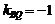 .
.
因为 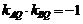 ,
,
所以 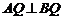 .
.
所以 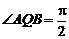 .
…………6分
.
…………6分
(ⅱ)当直线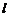 与
与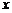 轴不垂直时,由题意可设直线
轴不垂直时,由题意可设直线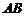 的方程为
的方程为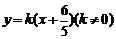 .
.
由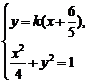 消去
消去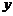 得:
得: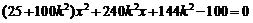 .
.
因为 点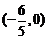 在椭圆
在椭圆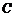 的内部,显然
的内部,显然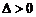 .
.
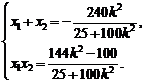 ……………8分
……………8分
因为 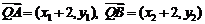 ,
,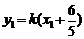 ,
,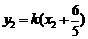 ,
,
所以 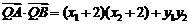
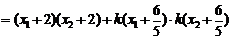
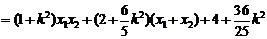
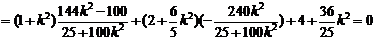 .
.
所以 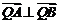 .
.
所以 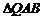 为直角三角形.
………………11分
为直角三角形.
………………11分
 (III)假设存在直线
(III)假设存在直线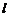 使得
使得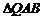 为等腰三角形,则
为等腰三角形,则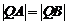 .
.
取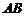 的中点
的中点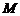 ,连接
,连接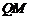 ,则
,则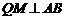 .
.
记点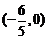 为
为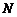 .
.
另一方面,点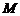 的横坐标
的横坐标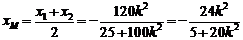 ,
,
所以 点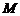 的纵坐标
的纵坐标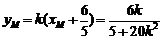 .
.
所以 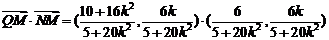
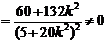 .
.
所以 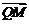 与
与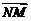 不垂直,矛盾.
不垂直,矛盾.
所以 当直线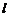 与
与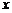 轴不垂直时,不存在直线
轴不垂直时,不存在直线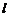 使得
使得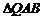 为等腰三角形.…………13分
为等腰三角形.…………13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
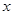 轴上的椭圆
轴上的椭圆 和双曲线
和双曲线 的离心率互为倒数,它们在第一象限交点的坐标为
的离心率互为倒数,它们在第一象限交点的坐标为 ,设直线
,设直线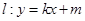 (其中
(其中 为整数).
为整数). 和双曲线
和双曲线 的标准方程;
的标准方程; 与椭圆
与椭圆 ,与双曲线
,与双曲线 ,问是否存在直线
,问是否存在直线 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. 轴上的椭圆的离心率为
轴上的椭圆的离心率为 ,它的长轴长等于圆
,它的长轴长等于圆 的半径,则椭圆的标准方程是( )
的半径,则椭圆的标准方程是( ) B.
B.  C.
C.
 D.
D.
 轴上的椭圆
轴上的椭圆 过点
过点 ,且离心率为
,且离心率为 ,
, 为椭圆
为椭圆 的直线
的直线 与椭圆
与椭圆 ,
, 两点.
两点. 的大小;
的大小;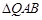 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线 轴上的椭圆
轴上的椭圆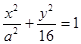 的两个焦点分别为
的两个焦点分别为 , 且
, 且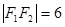 ,弦
,弦 过焦点
过焦点 ,则
,则 的周长为
的周长为 B.
B.  C.
C.  D.
D. 